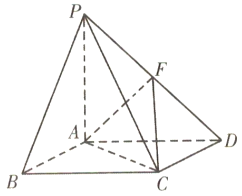
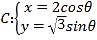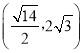题目内容
【题目】某市为提升中学生的数学素养,激发学生学习数学的兴趣,举办了一次“数学文化知识大赛”,分预赛和复赛两个环节.已知共有8000名学生参加了预赛,现从参加预赛的全体学生中随机地抽取100人的预赛成绩作为样本,得到如下频率分布直方图.

(1)规定预赛成绩不低于80分为优良,若从上述样本中预赛成绩不低于60分的学生中随机地抽取2人,求恰有1人预赛成绩优良的概率;
(2)由频率分布直方图可认为该市全体参加预赛学生的预赛成绩Z服从正态分布N(μ,σ2),其中μ可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且σ2=362.利用该正态分布,估计全市参加预赛的全体学生中预赛成绩不低于91分的人数;
(3)预赛成绩不低于91分的学生将参加复赛,复赛规则如下:①每人的复赛初始分均为100分;②参赛学生可在开始答题前自行决定答题数量n,每一题都需要“花”掉(即减去)一定分数来获取答题资格,规定答第k题时“花”掉的分数为0.1k(k∈(1,2n));③每答对一题加1.5分,答错既不加分也不减分;④答完n题后参赛学生的最终分数即为复赛成绩.已知学生甲答对每道题的概率均为0.7,且每题答对与否都相互独立.若学生甲期望获得最佳的复赛成绩,则他的答题数量n应为多少?
(参考数据:![]() ;若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)≈0.6827,P(μ﹣2σ<Z<μ+2σ)≈0.9545,P(μ﹣3σ<Z<μ+3σ)≈0.9973.
;若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)≈0.6827,P(μ﹣2σ<Z<μ+2σ)≈0.9545,P(μ﹣3σ<Z<μ+3σ)≈0.9973.
【答案】(1)![]() (2)182;(3)n应该是10.
(2)182;(3)n应该是10.
【解析】
(1)求出样本中成绩不低于60分的学生共有40人,其中成绩优良的人数为15人,由此能求出恰有1人预赛成绩优良的概率.
(2)根据频率分布直方图求得样本中的100名学生预赛成绩的平均值![]() 53,则μ=53,由σ2=362,得σ=19,从而P(Z≥91)=P(Z≥μ+2σ)求解.
53,则μ=53,由σ2=362,得σ=19,从而P(Z≥91)=P(Z≥μ+2σ)求解.
(3)以随机变量ξ表示甲答对的题数,则ξ~B(n,0.7),且Eξ=0.7n,记甲答完n题所加的分数为随机变量X,则X=1.5ξ,EX=1.5Eξ=1.05n,为了获取答n题的资格,甲需要“花”掉的分数为:0.1×(1+2+3+…+n)=0.05(n2+n),设甲答完n题的分数为M(n),则M(n)=100﹣0.05(n2+n)+1.05n=﹣0.05(n﹣10)2+105,由此能求出学生甲期望获得最佳复赛成绩的答题量n的值.
(1)由题意得样本中成绩不低于60分的学生共有:
(0.0125+0.0075)×20×100=40人,
其中成绩优良的人数为0.0075×20×100=15人,
记“从样本中预赛成绩不低于60分的学生中随机地抽取2人,恰有1人预赛成绩优良”为事件C,
则恰有1人预赛成绩优良的概率:
P(C)![]() .
.
(2)由题意知样本中的100名学生预赛成绩的平均值为:
![]() 10×0.1+30×0.2+50×0.3+70×0.25+90×0.15=53,则μ=53,
10×0.1+30×0.2+50×0.3+70×0.25+90×0.15=53,则μ=53,
又由σ2=362,∴σ=19,
∴P(Z≥91)=P(Z≥μ+2σ)![]() 0.02275,
0.02275,
∴估计全市参加参赛的全体学生中成绩不低于91分的人数为:
8000×0.02275=182,
即全市参赛学生中预赛成绩不低于91分的人数为182.
(3)以随机变量ξ表示甲答对的题数,则ξ~B(n,0.7),且Eξ=0.7n,
记甲答完n题所加的分数为随机变量X,则X=1.5ξ,
∴EX=1.5Eξ=1.05n,
依题意为了获取答n题的资格,甲需要“花”掉的分数为:
0.1×(1+2+3+…+n)=0.05(n2+n),
设甲答完n题的分数为M(n),
则M(n)=100﹣0.05(n2+n)+1.05n=﹣0.05(n﹣10)2+105,
由于n∈N*,∴当n=10时,M(n)取最大值105,即复赛成绩的最大值为105.
∴若学生甲期望获得最佳复赛成绩,则他的答题量n应该是10.

 名校课堂系列答案
名校课堂系列答案【题目】![]() 年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的
年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的![]() 次线上测试成绩进行统计如图所示:
次线上测试成绩进行统计如图所示:
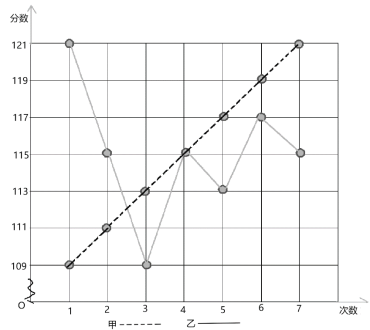
(1)请填写下表(要求写出计算过程)
平均数 | 方差 | |
甲 | ||
乙 |
(2)从下列三个不同的角度对这次方案选择的结果进行
①从平均数和方差相结合看(分析哪种方案的成绩更好);
②从折线图上两种方案的走势看(分析哪种方案更有潜力).