题目内容
【题目】已知点
关于坐标原点
对称，
，以
为圆心的圆过两点，且与直线
相切.若存在定点
，使得当
运动时，
为定值，则点的坐标为（ ）
A.
B.
C.
D.
【答案】D
【解析】
根据圆的几何性质，结合圆的切线性质、勾股定理，通过计算可以判断出点
的轨迹是抛物线，再根据抛物线的定义进行求解即可.
设
，因为点
关于坐标原点
对称，所以是线段
的中点，
又因为以为圆心的圆过两点，所以有
，
因此有
，因为点关于坐标原点对称，
，
所以
.
又因为以为圆心的圆与直线
相切，所以有
，
把、代入中，得：
，化简得：
，因此点的轨迹是抛物线，
该抛物线的焦点坐标为
，准线方程为：
，
，
由抛物线的定义可知：
，
所以有
，
由题意可知存在定点
，使得当
运动时，
为定值，
因此一定有
，此时定点是该抛物线的焦点.
故选：D
练习册系列答案
相关题目
【题目】
年初新冠病毒疫情爆发，全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略：先采取甲、乙两套方案教学，并对分别采取两套方案教学的班级的
次线上测试成绩进行统计如图所示：
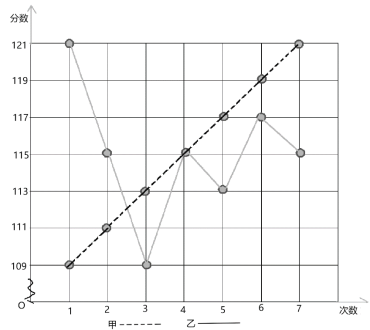
（1）请填写下表（要求写出计算过程）
平均数 | 方差 | |
甲 | ||
乙 |
（2）从下列三个不同的角度对这次方案选择的结果进行
①从平均数和方差相结合看（分析哪种方案的成绩更好）；
②从折线图上两种方案的走势看（分析哪种方案更有潜力）.
