题目内容
8．已知函数f（x）=$\frac{x（{a}^{x}-1）}{{a}^{x}+1}$（a＞0，a≠1），则（ ）| A． | 函数f（x）在（0，+∞）上是增函数 | B． | 函数f（x）在（0，+∞）上是减函数 | ||
| C． | 函数f（x）是奇函数 | D． | 函数f（x）是偶函数 |
分析 根据函数奇偶性的定义进行判断即可．
解答 解：函数的定义域为R，
则f（-x）=$\frac{-x（{a}^{-x}-1）}{{a}^{-x}+1}$=$\frac{-x（1-{a}^{x}）}{1+{a}^{x}}$=$\frac{x（{a}^{x}-1）}{{a}^{x}+1}$=f（x），
则函数f（x）是偶函数，
故选：D．
点评 本题主要考查函数奇偶性的判断，根据函数奇偶性的定义是解决本题的关键．
练习册系列答案
相关题目
18．在如图所示的程序框图中，若输出的S值等于16，则在该程序框图中的判断框内填写的条件为（ ）
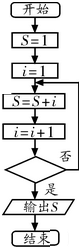
| A． | i＞5 | B． | i＞6 | C． | i＞7 | D． | i＞8 |
16．某同学为了计算函数y=lnx图象与x轴，直线x=1，x=e所围成形状A的面积，采用“随机模拟方法”，用计算机分别产生10个在[1，e]上的均匀随机数xi（1≤i≤10）和10个在[0，1]上的均匀随机数yi（1≤i≤10），其数据记录为如下表的前两行．
（1）依次表格中的数据回答，在图形A内的点有多少个，分别是什么？
（2）估算图形A的面积．
| xi | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| yi | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| lnxi | 0.92 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
（2）估算图形A的面积．
在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，且PA⊥平面ABCD，点M是棱PA的中点．