题目内容
5.若2sin2($\frac{π}{4}$+$\frac{x}{2}$)=1-cos(π-x),则sin2x=( )| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
分析 由三角函数中的恒等变换应用化简已知等式可得sinx=cosx,从而可得2x=2k$π+\frac{π}{2}$,k∈Z,从而可求sin2x的值.
解答 解:∵2sin2($\frac{π}{4}$+$\frac{x}{2}$)=1-cos(π-x),
∴1-cos($\frac{π}{2}$+x)=1+cosx,
∴1+sinx=1+cosx,即可解得:sinx=cosx.
∴解得:x=k$π+\frac{π}{4}$,k∈Z,即2x=2k$π+\frac{π}{2}$,k∈Z,
∴sin2x=sin(2k$π+\frac{π}{2}$)=1,
故选:D.
点评 本题主要考查了三角函数中的恒等变换应用和特殊角的三角函数求值,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.某同学为了计算函数y=lnx图象与x轴,直线x=1,x=e所围成形状A的面积,采用“随机模拟方法”,用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行.
(1)依次表格中的数据回答,在图形A内的点有多少个,分别是什么?
(2)估算图形A的面积.
| xi | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| yi | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| lnxi | 0.92 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
(2)估算图形A的面积.
10.已知i为虚数单位,若$\frac{1+i}{z}=1-2i$,则复数z所对应的点所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.下列说法中正确的是( )
| A. | 若命题p:?x∈R有x2>0,则¬p:?x∈R有x2≤0 | |
| B. | 若p是q的充分不必要条件,则¬p是¬q的必要不充分条件 | |
| C. | 若命题p:$\frac{1}{x-1}$>0,则¬p:$\frac{1}{x-1}$≤0 | |
| D. | 方程ax2+x+a=0有唯一解的充要条件是a=±$\frac{1}{2}$ |
15.实数X,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+3y-3≥0\\ 3x+y-9≤0\end{array}\right.$,若z=ax+y的最大值为2a+3,则a的取值范围是( )
| A. | [-3,1] | B. | [-1,3] | C. | (-∞,1] | D. | [3,+∞) |
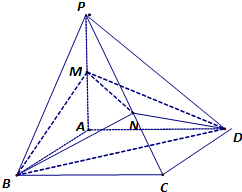 在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,且PA⊥平面ABCD,点M是棱PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,且PA⊥平面ABCD,点M是棱PA的中点.