题目内容
(本小题满分16分)已知数列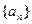 是以
是以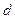 为公差的等差数列,数列
为公差的等差数列,数列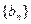 是以
是以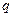 为公比的等比数列.(Ⅰ)若数列
为公比的等比数列.(Ⅰ)若数列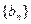 的前
的前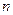 项和为
项和为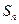 ,且
,且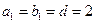 ,
,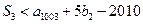 ,求整数
,求整数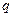 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问数列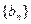 中是否存在一项
中是否存在一项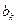 ,使得
,使得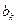 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续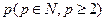 项的和?请说明理由;(Ⅲ)若
项的和?请说明理由;(Ⅲ)若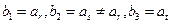 (其中
(其中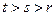 ,且(
,且(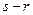 )是(
)是(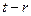 )的约数),求证:数列
)的约数),求证:数列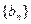 中每一项都是数列
中每一项都是数列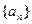 中的项.
中的项.
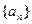 是以
是以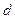 为公差的等差数列,数列
为公差的等差数列,数列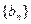 是以
是以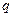 为公比的等比数列.(Ⅰ)若数列
为公比的等比数列.(Ⅰ)若数列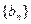 的前
的前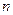 项和为
项和为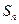 ,且
,且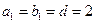 ,
,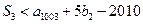 ,求整数
,求整数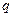 的值;
的值;(Ⅱ)在(Ⅰ)的条件下,试问数列
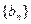 中是否存在一项
中是否存在一项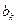 ,使得
,使得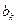 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续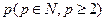 项的和?请说明理由;(Ⅲ)若
项的和?请说明理由;(Ⅲ)若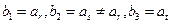 (其中
(其中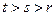 ,且(
,且(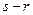 )是(
)是(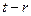 )的约数),求证:数列
)的约数),求证:数列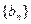 中每一项都是数列
中每一项都是数列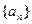 中的项.
中的项.(Ⅰ)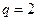 (Ⅱ) 不存在 (Ⅲ)见解析
(Ⅱ) 不存在 (Ⅲ)见解析
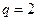 (Ⅱ) 不存在 (Ⅲ)见解析
(Ⅱ) 不存在 (Ⅲ)见解析(Ⅰ)由题意知,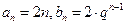 ,所以由
,所以由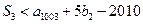 ,
,
得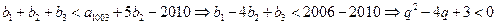 ……3分
……3分
解得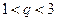 ,又
,又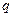 为整数,所以
为整数,所以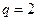 ………………………………………………………5分
………………………………………………………5分
(Ⅱ)假设数列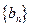 中存在一项
中存在一项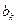 ,满足
,满足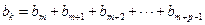 ,
,
因为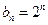 ,∴
,∴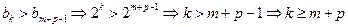 (*)…………8分
(*)…………8分
又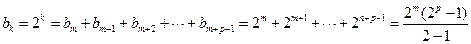
=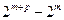
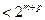 ,所以
,所以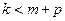 ,此与(*)式矛盾. 所以,这要的项
,此与(*)式矛盾. 所以,这要的项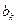 不存在……11分
不存在……11分
(Ⅲ)由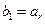 ,得
,得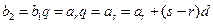 ,则
,则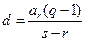 ………………12分
………………12分
又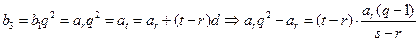 ,
,
从而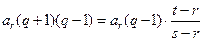 ,因为
,因为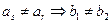 ,所以
,所以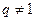 ,又
,又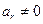 ,
,
故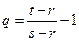 . 又
. 又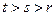 ,且(
,且(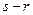 )是(
)是(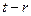 )的约数,所以
)的约数,所以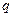 是整数,且
是整数,且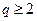 ………14分
………14分
对于数列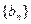 中任一项
中任一项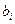 (这里只要讨论
(这里只要讨论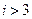 的情形),有
的情形),有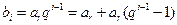
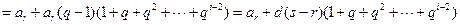
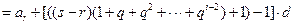 ,
,
由于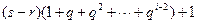 是正整数,所以
是正整数,所以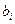 一定是数列
一定是数列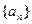 的项……………16分
的项……………16分
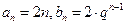 ,所以由
,所以由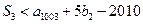 ,
,得
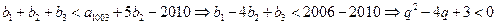 ……3分
……3分解得
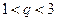 ,又
,又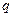 为整数,所以
为整数,所以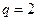 ………………………………………………………5分
………………………………………………………5分(Ⅱ)假设数列
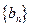 中存在一项
中存在一项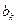 ,满足
,满足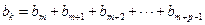 ,
,因为
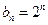 ,∴
,∴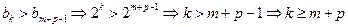 (*)…………8分
(*)…………8分又
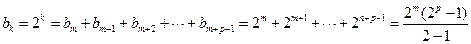
=
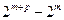
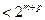 ,所以
,所以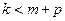 ,此与(*)式矛盾. 所以,这要的项
,此与(*)式矛盾. 所以,这要的项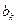 不存在……11分
不存在……11分(Ⅲ)由
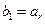 ,得
,得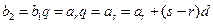 ,则
,则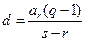 ………………12分
………………12分又
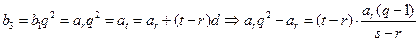 ,
,从而
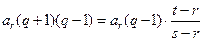 ,因为
,因为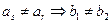 ,所以
,所以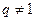 ,又
,又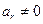 ,
,故
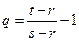 . 又
. 又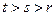 ,且(
,且(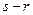 )是(
)是(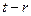 )的约数,所以
)的约数,所以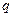 是整数,且
是整数,且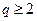 ………14分
………14分对于数列
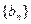 中任一项
中任一项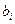 (这里只要讨论
(这里只要讨论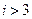 的情形),有
的情形),有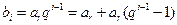
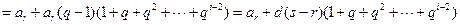
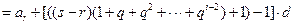 ,
,由于
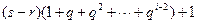 是正整数,所以
是正整数,所以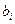 一定是数列
一定是数列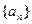 的项……………16分
的项……………16分
练习册系列答案
相关题目
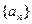 满足:
满足: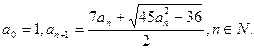
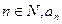 为正整数;(2)对任意
为正整数;(2)对任意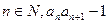 为完全平方数。
为完全平方数。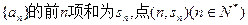 在函数
在函数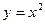 的图象上,数列
的图象上,数列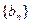 满足
满足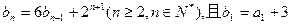 (1)求数列
(1)求数列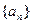 的通项公式;(2)证明列数
的通项公式;(2)证明列数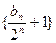 是等比数列,并求数列
是等比数列,并求数列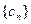 满足对任意的
满足对任意的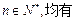
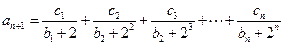 成立,
成立,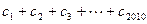 的值。
的值。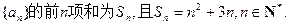
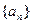 的通项公式; (II)求数列
的通项公式; (II)求数列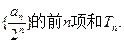
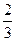 ,且
,且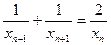 (n≥2),则xn等于( )
(n≥2),则xn等于( )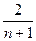
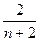
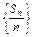 的前n项和,求Tn.
的前n项和,求Tn.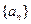
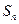
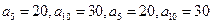
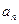 ; (2)若
; (2)若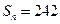 ,求n
,求n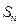 是等差数列
是等差数列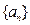 的前n项和,且S3=S8,Sk=S7,则k的值是( )
的前n项和,且S3=S8,Sk=S7,则k的值是( )