题目内容
【题目】如图，在四棱柱
中；
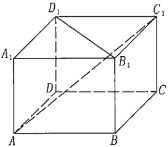
已知三个论断：（1）四棱柱是直四棱柱；（2）底面
是菱形；（3）
．
以其中两个论断作条件，余下一个为结论，可以得到三个命题，其中有几个是真命题？说明理由．
【答案】1个；理由见解析
【解析】
分别写出三个命题然后逐一判断．
解：以（1）、（2）作为条件，（3）为结论：即
为直四棱柱，底面为菱形，则侧棱
底面．
∴
在上底面上的射影为
．又底面为菱形，∴
．
由三垂线定理得
，这一命题为真．
以（2）、（3）为条件，（1）为结论：
为菱形，∴
．
又，∴
平面
．∴
．
但侧棱
未必垂直于底面．事实上，若侧棱倾斜，但保持与
垂直（这是可以做到的），则必符合条件（2）、（3），故此四棱柱不一定是直四棱柱．
若（1）、（3）为条件，（2）为结论：在底面上的射影为，又，由三垂线定理的逆定理得，即四边形的对角线互相垂直，但这样的四边形未必是菱形．
由以上分析知，真命题只有1个，即（1）（2）
（3）．
练习册系列答案
相关题目
