题目内容
【题目】已知函数![]() .(其中常数
.(其中常数![]() ,是自然对数的底数)
,是自然对数的底数)
(1)若![]() ,求
,求![]() 在
在![]() 上的极大值点;
上的极大值点;
(2)(![]() )证明
)证明![]() 在
在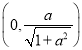 上单调递增;
上单调递增;
(![]() )求关于
)求关于![]() 的方程
的方程![]() 在
在![]() 上的实数解的个数.
上的实数解的个数.
【答案】(1)![]() ;(2)(
;(2)(![]() )证明见解析,(
)证明见解析,(![]() )当
)当![]() 时,方程
时,方程![]() 在
在![]() 上的实数解的个数为
上的实数解的个数为![]() ,当
,当![]() 时,方程
时,方程![]() 在
在![]() 上的实数解的个数为
上的实数解的个数为![]() .
.
【解析】
(1)首先求出函数的导数,利用导数得到函数的单调区间,再根据单调区间即可得到函数的极大值点.
(2)(![]() )首先根据
)首先根据![]() 的单调性只需证明
的单调性只需证明![]() ,将问题转化为证明
,将问题转化为证明![]() ,构造函数
,构造函数![]() ,再结合
,再结合![]() 的单调性即可证明.(ii)首先证明
的单调性即可证明.(ii)首先证明![]() ,再证明函数
,再证明函数![]() 的最大值
的最大值![]() ,设
,设![]() ,分别求出
,分别求出![]() 和
和![]() 的零点个数,从而得到方程解得个数.
的零点个数,从而得到方程解得个数.
(1)![]() .
.
当![]() 时,
时,![]() .
.
|
|
|
|
|
|
|
|
| 增函数 | 极大值 | 减函数 |
所以函数![]() 的极大值点为
的极大值点为![]() .
.
(2)(![]() )因为
)因为![]() ,所以在
,所以在![]() 上必存在唯一的实数
上必存在唯一的实数![]() ,使得
,使得![]() .
.
所以![]() ,
,![]() ,
,![]() 为增函数,
为增函数,
![]() ,
,![]() ,
,![]() 为减函数.
为减函数.
要证明![]() 在
在 上单调递增,只需证明
上单调递增,只需证明![]() 即可.
即可.
又因为![]() ,所以
,所以 ,
,
即证![]() 即可.
即可.
设![]() ,
,![]() ,所以
,所以![]() 在
在![]() 为减函数.
为减函数.
当![]() 时,
时,![]() ,
,![]() ,即
,即![]() ,
,
即证![]() ,
,
所以![]() 在
在 上单调递增.
上单调递增.
(![]() )先证明
)先证明![]() 时,
时,![]() .
.
设![]() ,
,![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() 在
在![]() 为增函数.
为增函数.
所以![]() ,即
,即![]() .
.
再证明函数![]() 的最大值
的最大值![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
所以![]() .
.
下面证![]() ,令
,令![]() ,则
,则![]() ,
,
即证![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() ,
,![]() ,
,
所以函数![]() 为增函数.
为增函数.
当![]() 时,
时,![]() ,即
,即![]() .
.
即证:![]() .
.
设![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
且![]() 在
在![]() 为减函数,所以
为减函数,所以![]() 在
在![]() 上有唯一零点.
上有唯一零点.
当![]() 时,
时,![]() ,
,![]() ,且
,且![]() 在
在![]() 为增函数.
为增函数.
①当![]() 时,
时,![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上没有零点.
上没有零点.
②当![]() 时,
时,![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上有唯一零点.
上有唯一零点.
综上所述:当![]() 时,方程
时,方程![]() 在
在![]() 上的实数解的个数为
上的实数解的个数为![]() ,
,
当![]() 时,方程
时,方程![]() 在
在![]() 上的实数解的个数为
上的实数解的个数为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某百货商店今年春节期间举行促销活动,规定消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商店经理对春节前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计,![]() 表示第
表示第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
(1)经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.请根据上表提供的数据,用最小二乘法求出
具有线性相关关系.请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)该商店规定:若抽中“一等奖”,可领取600元购物券;抽中“二等奖”可领取300元购物券;抽中“谢谢惠顾”,则没有购物券.已知一次抽奖活动获得“一等奖”的概率为![]() ,获得“二等奖”的概率为
,获得“二等奖”的概率为![]() .现有张、王两位先生参与了本次活动,且他们是否中奖相互独立,求此二人所获购物券总金额
.现有张、王两位先生参与了本次活动,且他们是否中奖相互独立,求此二人所获购物券总金额![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: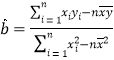 ,
,![]() ,
,![]() ,
,![]() .
.
【题目】下表为2016年至2019年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 | 1 | 2 | 3 | 4 |
线下销售额 | 95 | 165 | 230 | 310 |
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2020年该百货零售企业的线下销售额;
的线性回归方程,并预测2020年该百货零售企业的线下销售额;
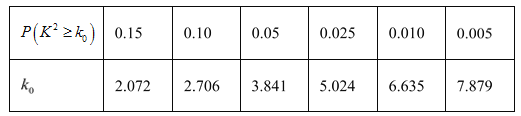
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了55位男顾客、50位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有10人、女顾客有20人,能否在犯错误的概率不超过0.025的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据:
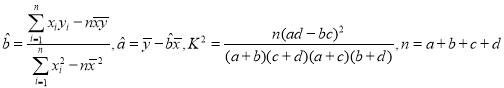 .
.