题目内容
某商场销售某种商品的经验表明,该商品每日的销售量y(单
位:千克)与销售价格x(单位:元/千克)满足关系式y=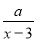 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
①求a的值;
②若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
①a=2②4元/千克
【解析】①因为x=5时,y=11,∴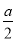 +10=11,∴a=2.
+10=11,∴a=2.
②由①知,y=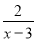 +10(x-6)2,
+10(x-6)2,
所以商场每日销售该商品所获得的利润f(x)=(x-3) 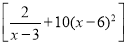 =2+10(x-3)(x-6)2,3<x<6.∴f′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-4)(x-6).
=2+10(x-3)(x-6)2,3<x<6.∴f′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-4)(x-6).
当3<x<4时,f′(x)>0;4<x<6时,f′(x)<0.∴f(x)在(3,4)上递增,(4,6)上递减.
当x=4时,f(x)取得最大值,f(4)=42.
即当销售价格为4元/千克时,商场每日销售该商品所获得利润最大.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目