题目内容
(本题满分16分)
函数f(x)=x3+3ax2+3bx+c在x=2处有极值,其图象在x=1处的切线平行于直线3x+y+2=0.
(1)求a,b的值; (2)求函数的极大值与极小值的差.
函数f(x)=x3+3ax2+3bx+c在x=2处有极值,其图象在x=1处的切线平行于直线3x+y+2=0.
(1)求a,b的值; (2)求函数的极大值与极小值的差.
(1)a=-1,b=0
(2)4
(2)4
(1)f¢(x)=3x2+6ax+3b.令f¢(x)=0,得3x2+6ax+3b=0(Ⅰ),因为f(x)在x=2处有极值,所以,x=2是方程(Ⅰ)的根,代入得4+4a+b=0 ①;又图象在x=1处的切线平行于直线3x+y+2=0,故y¢|x=1=-3,即3+6a+3b=-3 ②.所以由①,②解得a=-1,b=0.
(2)由(1)知f(x)=x3-3x2+c,f¢(x)=3x2-6x.f¢(x)=0的另一个根为x=0.列表如下:
因此,当x=0时,f(x)有极大值f(0)=c;当x=2时,f(x)有极小值f(2)=c-4.所以,所求的极大值与极小值之差为c-(c-4)=4.
(2)由(1)知f(x)=x3-3x2+c,f¢(x)=3x2-6x.f¢(x)=0的另一个根为x=0.列表如下:
| x | (-∞,0) | 0 | (0,2) | 2 | (2,+∞) |
| f¢(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
因此,当x=0时,f(x)有极大值f(0)=c;当x=2时,f(x)有极小值f(2)=c-4.所以,所求的极大值与极小值之差为c-(c-4)=4.

练习册系列答案
相关题目
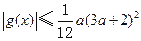
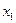 、
、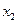
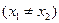 是函数
是函数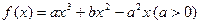 的两个极值点.
的两个极值点.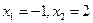 ,求函数
,求函数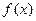 的解析式;
的解析式;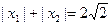 ,求
,求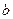 的最大值;
的最大值;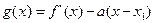 ,
,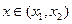 ,当
,当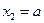 时,
时,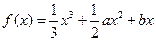 在区间
在区间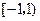 ,
,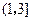 内各有一个极值点.
内各有一个极值点.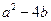 的最大值;
的最大值;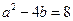 时,设函数
时,设函数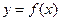 在点
在点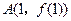 处的切线为
处的切线为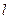 ,若
,若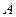 处穿过函数
处穿过函数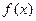 的表达式.
的表达式.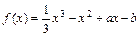 ,
,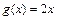 ,当
,当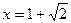 时,
时,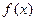 取得极值。
取得极值。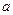 的值;
的值;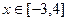 时,函数
时,函数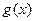 的图象有三个公共点,求
的图象有三个公共点,求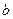 的取值范围。
的取值范围。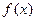 =
=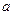
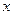 -
-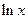 ,
,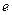 是自然常数,
是自然常数,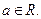
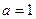 时, 求
时, 求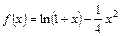 在
在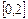 上的最大值和最小值。
上的最大值和最小值。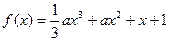 有极值的充要条件是 ( )
有极值的充要条件是 ( )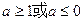
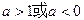

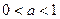
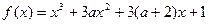 有极大值又有极小值,则
有极大值又有极小值,则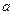 的取值范围是 .
的取值范围是 .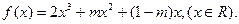
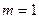 时,解不等式
时,解不等式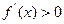 ;
;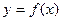 的所有切线中,切线斜率的最小值为
的所有切线中,切线斜率的最小值为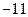 ,求
,求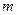 的值.
的值.