题目内容
(本小题满分13分)
已知函数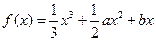 在区间
在区间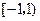 ,
,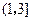 内各有一个极值点.
内各有一个极值点.
(I)求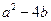 的最大值;
的最大值;
(II)当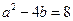 时,设函数
时,设函数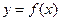 在点
在点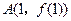 处的切线为
处的切线为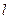 ,若
,若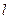 在点
在点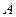 处穿过函数
处穿过函数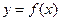 的图象(即动点在点
的图象(即动点在点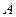 附近沿曲线
附近沿曲线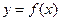 运动,经过点
运动,经过点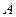 时,从
时,从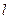 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数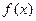 的表达式.
的表达式.
已知函数
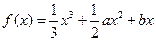 在区间
在区间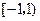 ,
,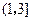 内各有一个极值点.
内各有一个极值点.(I)求
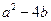 的最大值;
的最大值;(II)当
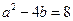 时,设函数
时,设函数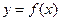 在点
在点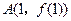 处的切线为
处的切线为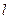 ,若
,若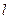 在点
在点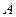 处穿过函数
处穿过函数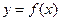 的图象(即动点在点
的图象(即动点在点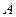 附近沿曲线
附近沿曲线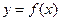 运动,经过点
运动,经过点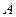 时,从
时,从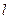 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数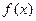 的表达式.
的表达式.(I)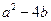 的最大值是16
的最大值是16
(II)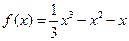 .
.
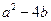 的最大值是16
的最大值是16(II)
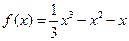 .
.解:(I)因为函数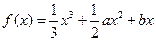 在区间
在区间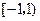 ,
,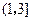 内分别有一个极值点,所以
内分别有一个极值点,所以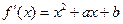
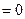 在
在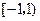 ,
,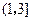 内分别有一个实根,
内分别有一个实根,
设两实根为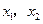 (
(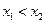 ),则
),则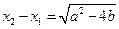 ,且
,且 .于是
.于是
 ,
,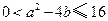 ,且当
,且当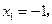
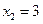 ,即
,即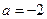 ,
,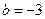 时等号成立.故
时等号成立.故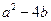 的最大值是16.
的最大值是16.
(II)解法一:由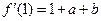 知
知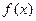 在点
在点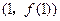 处的切线
处的切线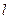 的方程是
的方程是
 ,即
,即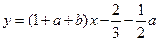 ,
,
因为切线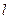 在点
在点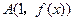 处空过
处空过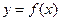 的图象,
的图象,
所以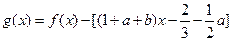 在
在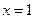 两边附近的函数值异号,则
两边附近的函数值异号,则
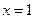 不是
不是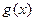 的极值点.
的极值点.
而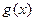
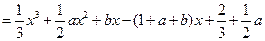 ,且
,且
 .
.
若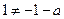 ,则
,则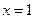 和
和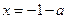 都是
都是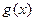 的极值点.
的极值点.
所以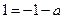 ,即
,即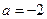 ,又由
,又由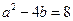 ,得
,得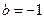 ,故
,故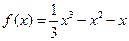 .
.
解法二:同解法一得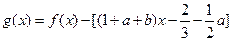
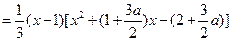 .
.
因为切线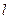 在点
在点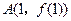 处穿过
处穿过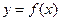 的图象,所以
的图象,所以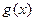 在
在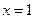 两边附近的函数值异号,于是存在
两边附近的函数值异号,于是存在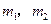 (
(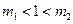 ).
).
当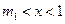 时,
时,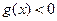 ,当
,当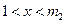 时,
时, ;
;
或当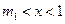 时,
时, ,当
,当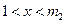 时,
时,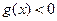 .
.
设 ,则
,则
当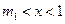 时,
时,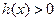 ,当
,当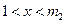 时,
时,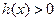 ;
;
或当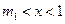 时,
时,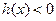 ,当
,当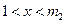 时,
时,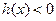 .
.
由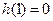 知
知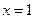 是
是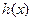 的一个极值点,则
的一个极值点,则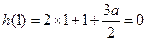 ,
,
所以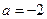 ,又由
,又由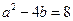 ,得
,得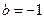 ,故
,故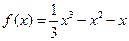 .
.
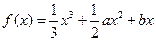 在区间
在区间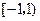 ,
,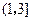 内分别有一个极值点,所以
内分别有一个极值点,所以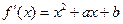
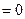 在
在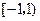 ,
,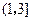 内分别有一个实根,
内分别有一个实根,设两实根为
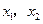 (
(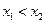 ),则
),则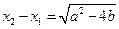 ,且
,且 .于是
.于是 ,
,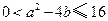 ,且当
,且当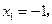
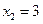 ,即
,即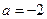 ,
,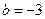 时等号成立.故
时等号成立.故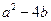 的最大值是16.
的最大值是16.(II)解法一:由
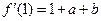 知
知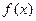 在点
在点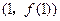 处的切线
处的切线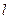 的方程是
的方程是 ,即
,即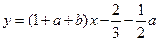 ,
,因为切线
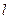 在点
在点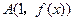 处空过
处空过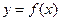 的图象,
的图象,所以
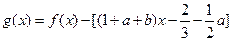 在
在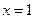 两边附近的函数值异号,则
两边附近的函数值异号,则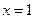 不是
不是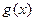 的极值点.
的极值点.而
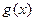
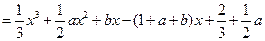 ,且
,且 .
.若
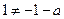 ,则
,则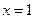 和
和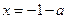 都是
都是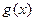 的极值点.
的极值点.所以
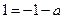 ,即
,即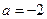 ,又由
,又由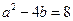 ,得
,得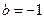 ,故
,故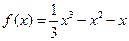 .
.解法二:同解法一得
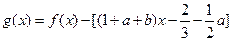
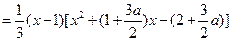 .
.因为切线
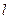 在点
在点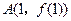 处穿过
处穿过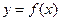 的图象,所以
的图象,所以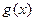 在
在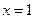 两边附近的函数值异号,于是存在
两边附近的函数值异号,于是存在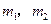 (
(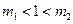 ).
).当
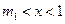 时,
时,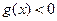 ,当
,当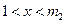 时,
时, ;
;或当
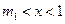 时,
时, ,当
,当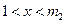 时,
时,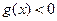 .
.设
 ,则
,则当
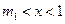 时,
时,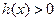 ,当
,当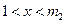 时,
时,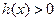 ;
;或当
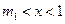 时,
时,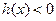 ,当
,当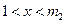 时,
时,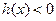 .
.由
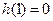 知
知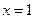 是
是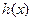 的一个极值点,则
的一个极值点,则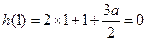 ,
,所以
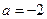 ,又由
,又由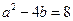 ,得
,得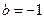 ,故
,故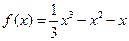 .
.
练习册系列答案
相关题目
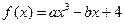 ,当
,当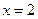 时,函数
时,函数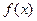 有极值为
有极值为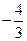 ,
,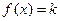 有3个解,求实数
有3个解,求实数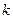 的取值范围。
的取值范围。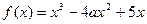 (
(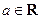 ).
).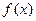 在区间[0, 2]上无极值, 求a的取值范围.
在区间[0, 2]上无极值, 求a的取值范围.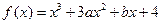 在
在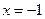 时有极值0,则常数
时有极值0,则常数 .
.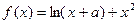
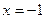 时,
时,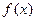 取得极值,求
取得极值,求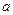 值,并讨论
值,并讨论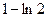
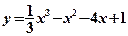 ,直线
,直线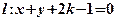 ,当
,当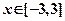 时,直线
时,直线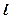 恒在曲线C的上方,则实数
恒在曲线C的上方,则实数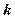 的取值范围是 ( )
的取值范围是 ( )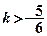
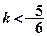
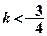
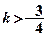
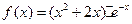 ,关于
,关于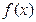 给出下列四个命题;
给出下列四个命题;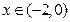 时,
时,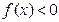 ;
;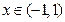 时,
时,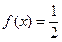 有且只有三个实数解.
有且只有三个实数解.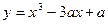 在(1,2)内有极小值,则实数a的取值范围是( )
在(1,2)内有极小值,则实数a的取值范围是( )


