题目内容
(本题满分12分)
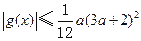
设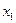 、
、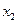
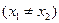 是函数
是函数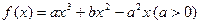 的两个极值点.
的两个极值点.
(1)若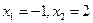 ,求函数
,求函数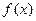 的解析式;
的解析式;
(2)若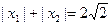 ,求
,求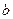 的最大值;
的最大值;
(3)设函数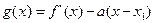 ,
,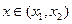 ,当
,当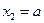 时,
时,
求证:
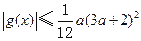
设
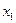 、
、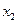
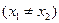 是函数
是函数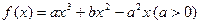 的两个极值点.
的两个极值点.(1)若
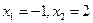 ,求函数
,求函数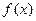 的解析式;
的解析式;(2)若
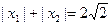 ,求
,求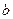 的最大值;
的最大值;(3)设函数
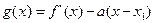 ,
,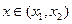 ,当
,当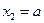 时,
时,求证:
(1)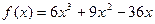
(2)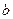 的最大值为
的最大值为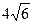
(3)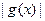
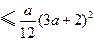 成立
成立
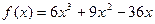
(2)
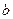 的最大值为
的最大值为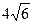
(3)
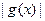
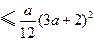 成立
成立(I)∵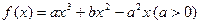 ,∴
,∴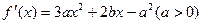
依题意有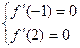 ,∴
,∴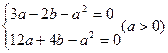 .
.
解得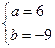 ,∴
,∴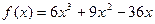 . .
. .
(II)∵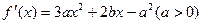 ,
,
依题意,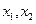 是方程
是方程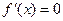 的两个根,且
的两个根,且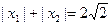 ,
,
∴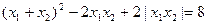 .
.
∴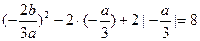 ,∴
,∴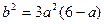 .
.
∵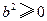 ∴
∴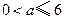 .
.
设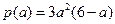 ,则
,则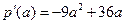 .
.
由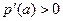 得
得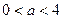 ,由
,由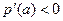 得
得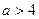 .
.
即:函数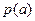 在区间
在区间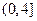 上是增函数,在区间
上是增函数,在区间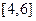 上是减函数,
上是减函数,
∴当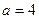 时,
时,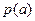 有极大值为96,∴
有极大值为96,∴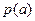 在
在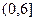 上的最大值是96,
上的最大值是96,
∴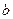 的最大值为
的最大值为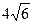 .
.
(III) 证明:∵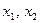 是方程
是方程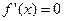 的两根,
的两根,
∴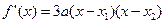 .
.
∵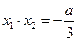 ,
,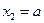 ,∴
,∴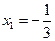 .
.
∴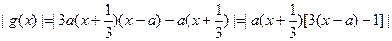
∵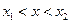 ,即
,即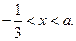 ∴
∴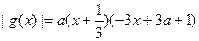 ∴
∴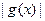
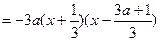
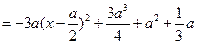
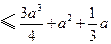
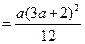 .
.
∴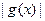
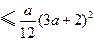 成立.
成立.
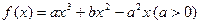 ,∴
,∴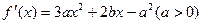
依题意有
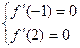 ,∴
,∴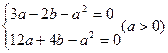 .
. 解得
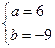 ,∴
,∴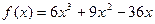 . .
. . (II)∵
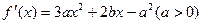 ,
,依题意,
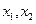 是方程
是方程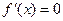 的两个根,且
的两个根,且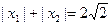 ,
,∴
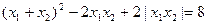 .
.∴
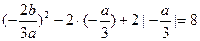 ,∴
,∴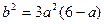 .
.∵
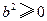 ∴
∴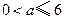 .
.设
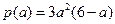 ,则
,则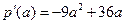 .
.由
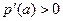 得
得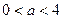 ,由
,由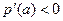 得
得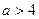 .
.即:函数
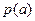 在区间
在区间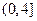 上是增函数,在区间
上是增函数,在区间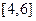 上是减函数,
上是减函数,∴当
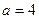 时,
时,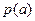 有极大值为96,∴
有极大值为96,∴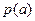 在
在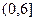 上的最大值是96,
上的最大值是96,∴
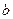 的最大值为
的最大值为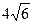 .
. (III) 证明:∵
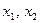 是方程
是方程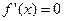 的两根,
的两根,∴
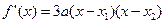 .
. ∵
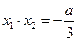 ,
,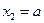 ,∴
,∴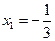 .
.∴
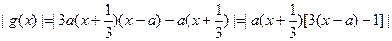
∵
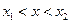 ,即
,即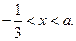 ∴
∴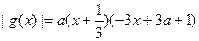 ∴
∴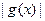
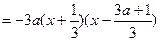
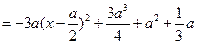
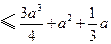
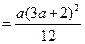 .
. ∴
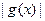
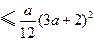 成立.
成立.
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
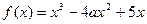 (
(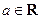 ).
).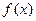 在区间[0, 2]上无极值, 求a的取值范围.
在区间[0, 2]上无极值, 求a的取值范围.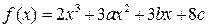 在
在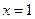 及
及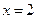 时取得极值,
时取得极值,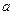 、
、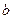 的值;
的值;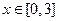 ,都有
,都有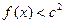 成立,求c的取值范围.
成立,求c的取值范围.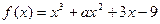 ,已知
,已知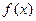 在
在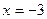 时取得极值,则
时取得极值,则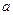 = ▲ .
= ▲ .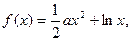
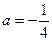 时,求
时,求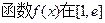 上的最大值、最小值:
上的最大值、最小值: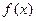 的单调区间;
的单调区间;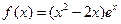 的判断正确的是 ( )
的判断正确的是 ( )
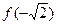 是极小值,
是极小值,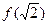 是极大值
是极大值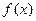 有最小值,没有最大值
有最小值,没有最大值 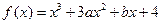 在
在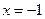 时有极值0,则常数
时有极值0,则常数 .
.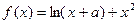
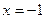 时,
时,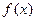 取得极值,求
取得极值,求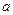 值,并讨论
值,并讨论