题目内容
(13分)已知,A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于EF两点,交抛物线于M.N两点,交y轴于B.C两点
(1)当A点坐标为(8,4)时,求直线EF的方程;
(2)当A点坐标为(2,2)时,求直线MN的方程;
(3)当A点的横坐标大于2时,求△ABC面积的最小值。
(1)当A点坐标为(8,4)时,求直线EF的方程;
(2)当A点坐标为(2,2)时,求直线MN的方程;
(3)当A点的横坐标大于2时,求△ABC面积的最小值。

(1)7x+4y-8=0
(2)3x+2y-2=0
(3)8
(1)∵DEFA四点共圆
EF是圆(x-1)2+y2=1及(x-1)(x-8)+y(y-4)=0的公共弦
∴EF的方程为7x+4y-8=0………………………………………………4分
(2)设AM的方程为y-2=k(x-2)
即kx-y+2-2k=0与圆(x-1)2+y2=1相切得
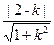 =1
=1∴k=
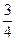
把y-2=
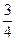 (x-2)代入y2=2x得M(
(x-2)代入y2=2x得M(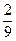 ,
,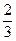 ),而N(2,-2)
),而N(2,-2)∴MN的方程为3x+2y-2=0………………………………………………8分
(3)设P(x0,y0),B(0,b),C(0,c),不妨设b>c,
直线PB的方程为y-b=
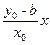 ,
,即(y0-b)x-x0y+x0b=0
又圆心(1,0)到PB的距离为1,所以
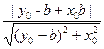 =1,故
=1,故(y0-b)2+x
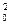 =(y0-b)2+2x0b(y0-b)+ x
=(y0-b)2+2x0b(y0-b)+ x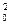 b2
b2又x0>2,上式化简得(x0-2)b2+2y0b-x0=0
同理有(x0-2)c2+2y0c-x0=0
故b,c是方程(x0-2)t2+2y0t-x0=0的两个实数根
所以b+c=
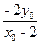 ,bc=
,bc=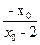 ,则(b-c)2=
,则(b-c)2=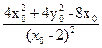
因为P(x0,y0)是抛物线上的点,所以有y
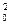 =2x0,则
=2x0,则(b-c)2=
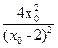 ,b-c=
,b-c=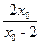 ,
,∴S△PBC=
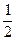 (b-c)x0=
(b-c)x0=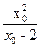 =x0-2+
=x0-2+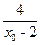 +4≥2
+4≥2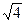 +4=8
+4=8当(x0-2)2=4时,上式取等号,此时x0=4,y=±2
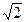
因此S△PBC的最小值为8…………………………………………………………13分

练习册系列答案
相关题目
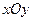 中,抛物线
中,抛物线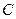 的顶点是坐标原点且经过点
的顶点是坐标原点且经过点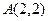 ,其焦点
,其焦点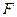 在
在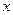 轴上,求抛物线方程.
轴上,求抛物线方程.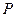 的轨迹
的轨迹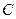 的方程;
的方程;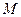 过定点
过定点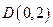 ,圆心
,圆心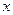 轴交于
轴交于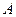 、
、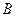 两点,设
两点,设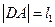 ,
,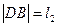 ,求
,求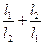 的最大值.
的最大值.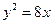 ,
,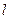 过抛物线的焦点
过抛物线的焦点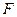 ,且垂直于
,且垂直于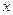 轴,
轴,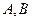 两点,求
两点,求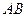 的长度。
的长度。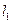 过抛物线的焦点
过抛物线的焦点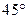 ,直线
,直线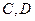 两点,
两点,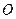 为原点。求△
为原点。求△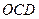 的面积。
的面积。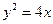 上点
上点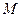 到焦点距离为3,则点
到焦点距离为3,则点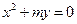 上的点到定点
上的点到定点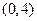 和到定直线
和到定直线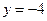 的距离相等,则
的距离相等,则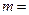
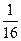 ;
;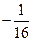 ;
;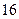 ;
;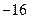 .
.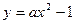 的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为
的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 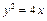 的准线与双曲线
的准线与双曲线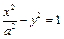 交于A、B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率为 .
交于A、B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率为 .