题目内容
19.已知直线y=x与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为P,椭圆的左、右焦点分别为F1、F2,且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,椭圆的离心率为e,则e2=( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{2-\sqrt{2}}{2}$ | D. | 2-$\sqrt{2}$ |
分析 利用已知条件求出P的坐标,代入椭圆方程,化简求解即可.
解答 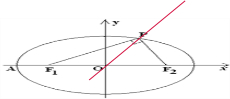 解:直线y=x与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为P,椭圆的左、右焦点分别为F1、F2,且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,
解:直线y=x与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为P,椭圆的左、右焦点分别为F1、F2,且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,
不妨设P(x,x),x>0可得:$\sqrt{2}x$=c,
则P$(\frac{\sqrt{2}}{2}c,\frac{\sqrt{2}}{2}c)$,代入椭圆方程可得:$\frac{{(\frac{\sqrt{2}}{2}c)}^{2}}{{a}^{2}}+\frac{{(\frac{\sqrt{2}}{2}c)}^{2}}{{b}^{2}}=1$,
即$\frac{1}{2}$e2+$\frac{1}{2}$•$\frac{{c}^{2}}{{b}^{2}}$=1.
即${e}^{2}+\frac{{c}^{2}}{{b}^{2}}=2$
可得${e}^{2}+\frac{{c}^{2}}{{a}^{2}-{c}^{2}}=2$.
${e}^{2}+\frac{{e}^{2}}{1-{e}^{2}}=2$,
解得:e2=2-$\sqrt{2}$.
故选:D.
点评 本题考查椭圆的离心率的求法,椭圆与向量的关系,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.三棱锥S-ABC的三视图如图,若点S,A,B,C都在球O的球面上,则球O的表面积是( )
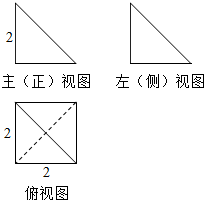

| A. | 4π | B. | 8π | C. | 12π | D. | 15π |
8.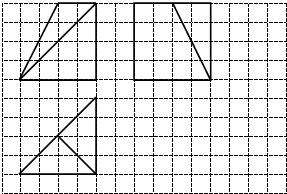 如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的体积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的体积为( )| A. | 40 | B. | $\frac{80}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{16}{3}$ |
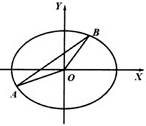 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F(1,0),是椭圆C的右焦点,若不经过原点O的直线l:y=kx+m(k>0)与椭圆C相交于不同的两点A、B,记直线OA,OB的斜率分别为k1,k2,且k1•k2=k2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F(1,0),是椭圆C的右焦点,若不经过原点O的直线l:y=kx+m(k>0)与椭圆C相交于不同的两点A、B,记直线OA,OB的斜率分别为k1,k2,且k1•k2=k2.