题目内容
10．三棱锥S-ABC的三视图如图，若点S，A，B，C都在球O的球面上，则球O的表面积是（ ）
| A． | 4π | B． | 8π | C． | 12π | D． | 15π |
分析 根据几何体的三视图，得出该几何体是棱长为2的正方体的四个顶点组成的三棱锥，由此求出它的外接球的直径，得出球的表面积即可．
解答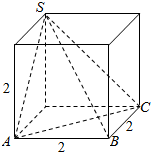 
解：根据几何体的三视图，得；
该几何体是由棱长为2的正方体的四个顶点组成的三棱锥，如图所示；
所以三棱锥的外接球的直径为2R=$\sqrt{{2}^{2}{+2}^{2}{+2}^{2}}$=2$\sqrt{3}$；
所以它的外接球的表面积为：
S=4πR2=π×${（2\sqrt{3}）}^{2}$=12π．
故选：C．
点评 本题考查了空间几何体的三视图的应用问题，解题的关键是求出外接球的直径，是基础题目．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
15．在△ABC中，若cosAcosBcosC＜0，则△ABC是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | ||
| C． | 钝角三角形 | D． | 锐角或钝角三角形 |
一个类似杨辉三角形的数阵：则第九行的第二个数为66．
19．已知直线y=x与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个交点为P，椭圆的左、右焦点分别为F1、F2，且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0，椭圆的离心率为e，则e2=（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{2-\sqrt{2}}{2}$ | D． | 2-$\sqrt{2}$ |