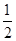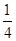题目内容
设函数f(x)=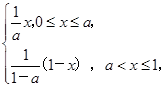 a为常数且a∈(0,1).
a为常数且a∈(0,1).
(1)当a= 时,求f
时,求f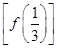 ;
;
(2)若x0满足f[f(x0)]=x0,但f(x0)≠x0,则称x0为f(x)的二阶周期点.证明函数f(x)有且仅有两个二阶周期点,并求二阶周期点x1,x2;
(3)对于(2)中的x1,x2,设A(x1,f[f(x1)]),B(x2,f[f(x2)]),C(a2,0),记△ABC的面积为S(a),求S(a)在区间[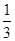 ,
, ]上的最大值和最小值.
]上的最大值和最小值.
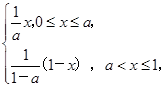 a为常数且a∈(0,1).
a为常数且a∈(0,1).(1)当a=
 时,求f
时,求f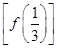 ;
; (2)若x0满足f[f(x0)]=x0,但f(x0)≠x0,则称x0为f(x)的二阶周期点.证明函数f(x)有且仅有两个二阶周期点,并求二阶周期点x1,x2;
(3)对于(2)中的x1,x2,设A(x1,f[f(x1)]),B(x2,f[f(x2)]),C(a2,0),记△ABC的面积为S(a),求S(a)在区间[
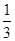 ,
, ]上的最大值和最小值.
]上的最大值和最小值.(1)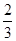 (2)见解析,x1=
(2)见解析,x1=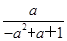 ,x2=
,x2=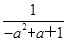 (3)最小值为
(3)最小值为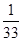 ,最大值为
,最大值为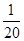
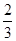 (2)见解析,x1=
(2)见解析,x1=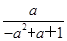 ,x2=
,x2=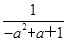 (3)最小值为
(3)最小值为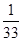 ,最大值为
,最大值为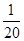
(1)当a= 时,f
时,f =
=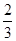 ,f
,f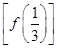 =f
=f =2
=2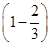 =
=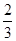 .
.
(2)证明:f[f(x)]=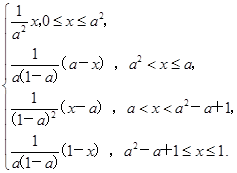
当0≤x≤a2时,由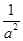 x=x解得x=0,由于f(0)=0,故x=0不是f(x)的二阶周期点;
x=x解得x=0,由于f(0)=0,故x=0不是f(x)的二阶周期点;
当a2<x≤a时,由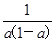 (a-x)=x解得x=
(a-x)=x解得x=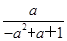 ∈(a2,a),因为f
∈(a2,a),因为f =
=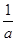 ·
· =
=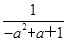 ≠
≠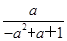 ,故x=
,故x=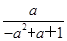 是f(x)的二阶周期点;
是f(x)的二阶周期点;
当a<x<a2-a+1时,由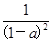 (x-a)=x解得x=
(x-a)=x解得x=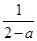 ∈(a,a2-a+1),
∈(a,a2-a+1),
因为f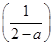 =
=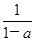 ·
·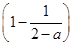 =
=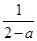 ,故x=
,故x=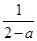 不是f(x)的二阶周期点;
不是f(x)的二阶周期点;
当a2-a+1≤x≤1时,由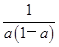 (1-x)=x解得x=
(1-x)=x解得x=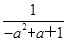 ∈(a2-a+1,1),因为f
∈(a2-a+1,1),因为f =
=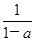 ·
·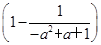 =
=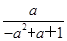 ≠
≠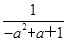 ,故x=
,故x=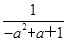 是f(x)的二阶周期点.
是f(x)的二阶周期点.
因此,函数f(x)有且仅有两个二阶周期点,x1=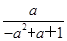 ,x2=
,x2=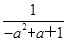 .
.
(3)由(2)得A(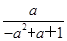 ,
,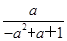 ),B(
),B(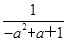 ,
,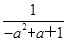 ),则S(a)=
),则S(a)=
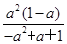 ,
,
S′(a)= ·
·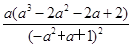 .
.
因为a∈[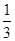 ,
, ],有a2+a<1,所以S′(a)=
],有a2+a<1,所以S′(a)= ·
·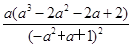 =
= ·
·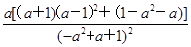 >0.(或令g(a)=a3-2a2-2a+2,g′(a)=3a2-4a-2=3(a-
>0.(或令g(a)=a3-2a2-2a+2,g′(a)=3a2-4a-2=3(a-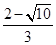 )(a-
)(a-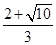 ),
),
因为a∈(0,1),所以g′(a)<0,则g(a)在区间[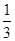 ,
, ]上最小值为g(
]上最小值为g( )=
)=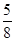 >0,故对于任意a∈[
>0,故对于任意a∈[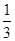 ,
, ],g(a)=a3-2a2-2a+2>0,S′(a)=
],g(a)=a3-2a2-2a+2>0,S′(a)= ·
·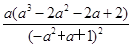 >0)则S(a)在区间[
>0)则S(a)在区间[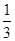 ,
, ]上单调递增,故S(a)在区间[
]上单调递增,故S(a)在区间[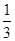 ,
, ]上的最小值为S(
]上的最小值为S(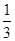 )=
)=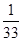 ,最大值为S(
,最大值为S( )=
)=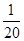 .
.
 时,f
时,f =
=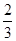 ,f
,f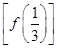 =f
=f =2
=2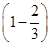 =
=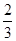 .
.(2)证明:f[f(x)]=
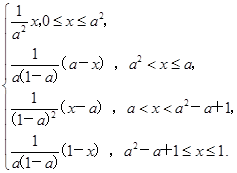
当0≤x≤a2时,由
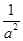 x=x解得x=0,由于f(0)=0,故x=0不是f(x)的二阶周期点;
x=x解得x=0,由于f(0)=0,故x=0不是f(x)的二阶周期点;当a2<x≤a时,由
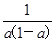 (a-x)=x解得x=
(a-x)=x解得x=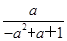 ∈(a2,a),因为f
∈(a2,a),因为f =
=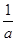 ·
· =
=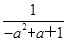 ≠
≠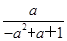 ,故x=
,故x=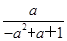 是f(x)的二阶周期点;
是f(x)的二阶周期点;当a<x<a2-a+1时,由
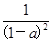 (x-a)=x解得x=
(x-a)=x解得x=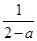 ∈(a,a2-a+1),
∈(a,a2-a+1),因为f
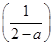 =
=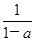 ·
·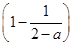 =
=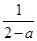 ,故x=
,故x=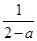 不是f(x)的二阶周期点;
不是f(x)的二阶周期点;当a2-a+1≤x≤1时,由
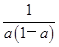 (1-x)=x解得x=
(1-x)=x解得x=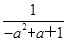 ∈(a2-a+1,1),因为f
∈(a2-a+1,1),因为f =
=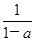 ·
·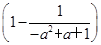 =
=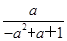 ≠
≠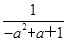 ,故x=
,故x=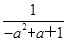 是f(x)的二阶周期点.
是f(x)的二阶周期点.因此,函数f(x)有且仅有两个二阶周期点,x1=
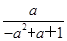 ,x2=
,x2=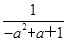 .
.(3)由(2)得A(
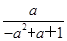 ,
,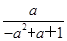 ),B(
),B(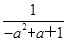 ,
,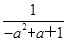 ),则S(a)=
),则S(a)=
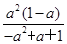 ,
,S′(a)=
 ·
·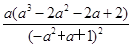 .
.因为a∈[
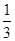 ,
, ],有a2+a<1,所以S′(a)=
],有a2+a<1,所以S′(a)= ·
·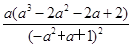 =
= ·
·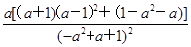 >0.(或令g(a)=a3-2a2-2a+2,g′(a)=3a2-4a-2=3(a-
>0.(或令g(a)=a3-2a2-2a+2,g′(a)=3a2-4a-2=3(a-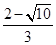 )(a-
)(a-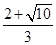 ),
),因为a∈(0,1),所以g′(a)<0,则g(a)在区间[
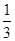 ,
, ]上最小值为g(
]上最小值为g( )=
)=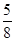 >0,故对于任意a∈[
>0,故对于任意a∈[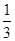 ,
, ],g(a)=a3-2a2-2a+2>0,S′(a)=
],g(a)=a3-2a2-2a+2>0,S′(a)= ·
·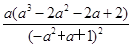 >0)则S(a)在区间[
>0)则S(a)在区间[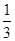 ,
, ]上单调递增,故S(a)在区间[
]上单调递增,故S(a)在区间[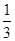 ,
, ]上的最小值为S(
]上的最小值为S(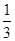 )=
)=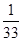 ,最大值为S(
,最大值为S( )=
)=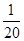 .
.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
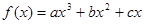 是
是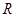 上的奇函数,且
上的奇函数,且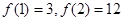
 的值
的值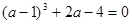 ,
,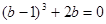 ,求
,求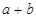 的值
的值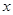 的不等式
的不等式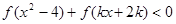 在
在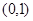 上恒成立,求
上恒成立,求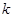 的取值范围
的取值范围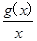 .
.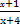 )的所有x之和为( )
)的所有x之和为( )

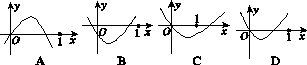
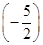 =( ).
=( ).