题目内容
2.若1<a<4,1<b<2,则$\frac{a}{b}$的取值范围为( )| A. | (1,2) | B. | ($\frac{1}{2}$,2) | C. | (2,4) | D. | ($\frac{1}{2}$,4) |
分析 作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.
解答 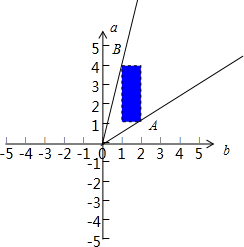 解:画出1<a<4,1<b<2,的可行域如图:则$\frac{a}{b}$的几何意义是可行域内的点与坐标原点连线的斜率,由可行域可知A(2,1),B(1,4),显然${k}_{OA}<\frac{a}{b}<{k}_{OB}$,而${k}_{OA}=\frac{1}{2}$,kOB=4,
解:画出1<a<4,1<b<2,的可行域如图:则$\frac{a}{b}$的几何意义是可行域内的点与坐标原点连线的斜率,由可行域可知A(2,1),B(1,4),显然${k}_{OA}<\frac{a}{b}<{k}_{OB}$,而${k}_{OA}=\frac{1}{2}$,kOB=4,
则$\frac{a}{b}$的取值范围为:($\frac{1}{2}$,4).
故选:D.
点评 本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.

练习册系列答案
相关题目
13.设f(x)=$\left\{\begin{array}{l}{x^t},x<2\\ 1o{g_t}({x^2}+7),x≥2\end{array}$,则$f(\sqrt{2})=4$,则f(3)=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
14.已知m,n都是非零实数,则“m=n”是“m2=n2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |

