题目内容
7.等差数列{an}中,an=2n-1,则其前n项和Sn=n2..分析 利用等差数列的前n项和公式即可得出.
解答 解:∵等差数列{an}中,an=2n-1,
∴a1=1.
∴Sn=$\frac{n(1+2n-1)}{2}$=n2.
故答案为:n2.
点评 本题考查了等差数列的前n项和公式,属于基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
17.已知直线x+y=1与圆x2+y2=1 相交A,B两点,则|AB|=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
18.定义:如果函数f(x)在[a,b]上存在x1,x2(a<x1<x2<b)满足$f'({x_1})=\frac{f(b)-f(a)}{b-a}$,$f'({x_2})=\frac{f(b)-f(a)}{b-a}$,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3-x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
| A. | $(\frac{1}{3},\frac{1}{2})$ | B. | ($\frac{3}{2},3$) | C. | ($\frac{1}{2}$,1) | D. | ($\frac{1}{3}$,1) |
15.已知抛物线y2=8x,P为其上一点,点N(5,0),点M满足|$\overrightarrow{MN}$|=1,$\overrightarrow{MN}$•$\overrightarrow{MP}$=0,则|$\overrightarrow{MP}$|的最小值为( )
| A. | $\sqrt{3}$ | B. | 4 | C. | $\sqrt{23}$ | D. | 2$\sqrt{6}$ |
2.若1<a<4,1<b<2,则$\frac{a}{b}$的取值范围为( )
| A. | (1,2) | B. | ($\frac{1}{2}$,2) | C. | (2,4) | D. | ($\frac{1}{2}$,4) |
12.阅读右边的程序框图,运行相应的程序,则输出s,k的值依次为( )
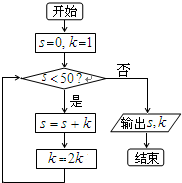

| A. | 32,63 | B. | 64,63 | C. | 63,32 | D. | 63,64 |
17.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=3,3$\overrightarrow{a}$+$\frac{1}{5}$$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$垂直,则$\overrightarrow{a}$,$\overrightarrow{b}$夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2}{3}$π | D. | $\frac{5}{6}$π |
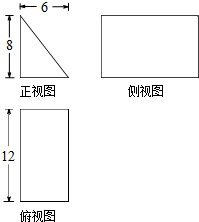
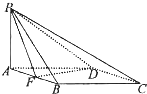 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,F是AB的中点.