题目内容
12.已知$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$都为单位向量,其中$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为$\frac{2}{3}$π,则$\sqrt{1-\overrightarrow{a}•\overrightarrow{b}}$+$\sqrt{1-\overrightarrow{b}•\overrightarrow{c}}$的取值范围是[$\frac{\sqrt{6}}{2}$,$\frac{\sqrt{6}}{2}$$+\sqrt{2}$].分析 根据平面向量的数量积得出则$\sqrt{1-\overrightarrow{a}•\overrightarrow{b}}$+$\sqrt{1-\overrightarrow{b}•\overrightarrow{c}}$=$\frac{\sqrt{6}}{2}$+$\sqrt{1-cosθ}$,利用三角函数的有界性求解即可.
解答 解:∵$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$都为单位向量,其中$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为$\frac{2}{3}$π,
∴$\overrightarrow{a}$$•\overrightarrow{b}$=$-\frac{1}{2}$,$\overrightarrow{b}$$•\overrightarrow{c}$=cosθ,θ∈[0,2π],
∴则$\sqrt{1-\overrightarrow{a}•\overrightarrow{b}}$+$\sqrt{1-\overrightarrow{b}•\overrightarrow{c}}$=$\frac{\sqrt{6}}{2}$+$\sqrt{1-cosθ}$,
∵-1≤cosθ≤1,
∴$\frac{\sqrt{6}}{2}$≤$\frac{\sqrt{6}}{2}$+$\sqrt{1-cosθ}$≤$\frac{\sqrt{6}}{2}$$+\sqrt{2}$,
故答案为:[$\frac{\sqrt{6}}{2}$,$\frac{\sqrt{6}}{2}$$+\sqrt{2}$]
点评 本题主要考查两个向量的数量积的定义,求向量的模,属于中档题

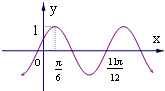 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象,如图所示,则将y=f(x)的图象向右平移$\frac{π}{3}$个单位后,得到的图象解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象,如图所示,则将y=f(x)的图象向右平移$\frac{π}{3}$个单位后,得到的图象解析式为( )| A. | y=sin(2x-$\frac{π}{6}$) | B. | y=cos2x | C. | y=sin(2x+$\frac{5π}{6}$) | D. | y=-cos2x |
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{30}}{10}$ |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
| A. | (1,2) | B. | ($\frac{1}{2}$,2) | C. | (2,4) | D. | ($\frac{1}{2}$,4) |
