题目内容
17.如图,在△ABC中,AB=$\sqrt{2}$,点D在边BC上,BD=2DC,cos∠DAC=$\frac{3\sqrt{10}}{10}$,cos∠C=$\frac{2\sqrt{5}}{5}$,则AC=$\sqrt{5}$.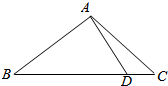
分析 根据三角形的边角关系结合正弦定理和余弦定理求出BD,CD和AD的长度,即可得到结论.
解答 解:∵BD=2DC,
∴设CD=x,AD=y,则BD=2x,
∵cos∠DAC=$\frac{3\sqrt{10}}{10}$,cos∠C=$\frac{2\sqrt{5}}{5}$,
∴sin∠DAC=$\frac{\sqrt{10}}{10}$,sin∠C=$\frac{\sqrt{5}}{5}$,
则由正弦定理得$\frac{AD}{sinC}=\frac{CD}{sin∠DAC}$,
即$\frac{y}{\frac{\sqrt{5}}{5}}=\frac{x}{\frac{\sqrt{10}}{10}}$,即y=$\sqrt{2}x$,
sin∠ADB=sin(∠DAC+∠C)=$\frac{\sqrt{10}}{10}$×$\frac{2\sqrt{5}}{5}$+$\frac{3\sqrt{10}}{10}$×$\frac{\sqrt{5}}{5}$=$\frac{\sqrt{2}}{2}$,
则∠ADB=$\frac{π}{4}$,$∠ADC=\frac{3π}{4}$,
在△ABD中,$A{B}^{2}=B{D}^{2}+A{D}^{2}-2AD•BDcos\frac{π}{4}$,
即2=4x2+2x2-2×$2x×\sqrt{2}x•\frac{\sqrt{2}}{2}$=2x2,
即x2=1,解得x=1,即BD=2,CD=1,AD=$\sqrt{2}$
在△ACD中,AC2=AD2+CD2-2AD•CDcos$\frac{3π}{4}$=2+1-2×$\sqrt{2}×(-\frac{\sqrt{2}}{2})$=5,
即AC=$\sqrt{5}$,
故答案为:$\sqrt{5}$.
点评 本题主要考查解三角形的应用,根据正弦定理和余弦定理是解决本题的关键.

| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{30}}{10}$ |
| A. | (-∞,0]∪(1,+∞) | B. | (-∞,0][1,+∞) | C. | (-∞,-1) | D. | (-∞,-1] |
| A. | (1,2) | B. | ($\frac{1}{2}$,2) | C. | (2,4) | D. | ($\frac{1}{2}$,4) |
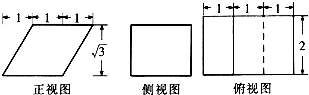
| A. | 8+2$\sqrt{3}$ | B. | 8+8$\sqrt{3}$ | C. | 12+4$\sqrt{3}$ | D. | 16+4$\sqrt{3}$ |
| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0≤x<2或x>4} | D. | {x|0<x≤2或x≥4} |
| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{12}$个单位长度 | D. | 向右平移$\frac{π}{12}$个单位长度 |
