Question

8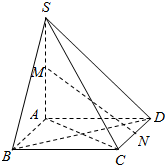．如图，在四棱锥S-ABCD中，底面ABCD是菱形，SA⊥平面ABCD，M，N分别为SA，CD的中点．
（I）证明：直线MN∥平面SBC；             
（Ⅱ）证明：平面SBD⊥平面SAC．

Answer 1

分析 （Ⅰ）取SB中点E，连接ME、CE，由三角形中位线定理、菱形性质得四边形MECN是平行四边形，由此能证明直线MN∥平面SBC．
（Ⅱ）连接AC、BD，交于点O，由线面垂直得SA⊥BD，由菱形性质得AC⊥BD，由此能证明平面SBD⊥平面SAC．

解答 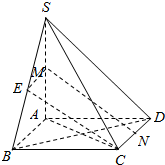（Ⅰ）证明：如图，取SB中点E，连接ME、CE，
因为M为SA的中点，所以ME∥AB，且ME=$\frac{1}{2}AB$，…（2分）
因为N为菱形ABCD边CD的中点，
所以CN∥AB，且CN=$\frac{1}{2}AB$，…（3分）
所以ME∥CN，ME=CN，
所以四边形MECN是平行四边形，
所以MN∥EC，…（5分）
又因为EC?平面SBC，MN?平面SBC，
所以直线MN∥平面SBC．…（6分）
（Ⅱ）证明：如图，连接AC、BD，交于点O，
因为SA⊥底面ABCD，所以SA⊥BD．…（7分）
因为四边形ABCD是菱形，所以AC⊥BD．…（8分）
又SA∩AC=A，所以BD⊥平面SAC．…（10分）
又BD?平面SBD，所以平面SBD⊥平面SAC．…（12分）

点评 本题考查线面平行的证明，考查面面垂直的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．