题目内容
11.比较两数log${\;}_{\frac{1}{4}}$$\frac{8}{7}$,log${\;}_{\frac{1}{5}}$$\frac{6}{5}$的大小.分析 由已知条件利用对数的性质、运算法则、换底公式和作商法能比较两数的大小.
解答 解:∵lg$\frac{7}{8}$>lg$\frac{5}{6}$,lg5>lg4,
∴log${\;}_{\frac{1}{4}}$$\frac{8}{7}$÷log${\;}_{\frac{1}{5}}$$\frac{6}{5}$=$\frac{lo{g}_{4}\frac{7}{8}}{lo{g}_{5}\frac{5}{6}}$=$\frac{lg\frac{7}{8}•lg5}{lg\frac{5}{6}•lg4}$>1,
∴log${\;}_{\frac{1}{4}}$$\frac{8}{7}$>log${\;}_{\frac{1}{5}}$$\frac{6}{5}$.
点评 本题考查两数大小的比较,是基础题,解题时要认真审题,注意对数的性质、运算法则、换底公式和作商法的合理运用.

练习册系列答案
相关题目
6.设集合A={x|$\frac{{x}^{2}}{2}$+y2=1},B={y|y=x2-1},则A∩B=( )
| A. | [-1,$\sqrt{2}$] | B. | {(-$\frac{\sqrt{6}}{2}$,$\frac{1}{2}$),($\frac{\sqrt{6}}{2}$,$\frac{1}{2}$)} | ||
| C. | {(-$\frac{\sqrt{6}}{2}$,$\frac{1}{2}$),($\frac{\sqrt{6}}{2}$,$\frac{1}{2}$),(0,1)} | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
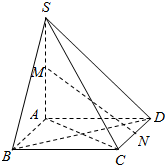 如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥平面ABCD,M,N分别为SA,CD的中点.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥平面ABCD,M,N分别为SA,CD的中点.