题目内容
3.已知函数f(x)=ax2-(2a+1)x+lnx,a∈R.(Ⅰ) 当a=1时,求f(x)的单调区间和极值;
(Ⅱ) 若关于x的方程f(x)=2ax2-2(a+1)x恰有两个不等的实根,求实数a的取值范围.
分析 (Ⅰ)当a=1时,函数f(x)=x2-3x+lnx,求出f(x)的导数,令f'(x)=0,列出表格即可得出函数的单调性,极值;
(Ⅱ)分离参数,构造函数$r(x)=\frac{lnx+x}{x^2}$,问题转化为使$y=\frac{lnx+x}{x^2}$与y=a恰有两个不同的交点,通过讨论a的范围即可求出.
解答 解(Ⅰ):当a=1时,函数f(x)=x2-3x+lnx,
则$f'(x)=\frac{{2{x^2}-3x+1}}{x}=\frac{(2x-1)(x-1)}{x}$.
令f'(x)=0,得${x_1}=\frac{1}{2}$,x2=1,
当x变化时,f'(x),f(x)的变化情况如下表:
| x | $(0{,_{\;}}\frac{1}{2})$ | $\frac{1}{2}$ | $(\frac{1}{2}{,_{\;}}1)$ | 1 | (1,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
当$x=\frac{1}{2}$时,f(x)极大值=f($\frac{1}{2}$)=-$\frac{5}{4}$-ln2,
当x=1时,f(x)极小值=f(1)=-2.
(Ⅱ)依题意ax2-(2a+1)x+lnx=2ax2-2(a+1)x,
即ax2-x-lnx=0.则$a=\frac{lnx+x}{x^2}$.
令$r(x)=\frac{lnx+x}{x^2}$,则$r'(x)=\frac{{(\frac{1}{x}+1){x^2}-2x(lnx+x)}}{x^4}=\frac{1-x-2lnx}{x^3}$.
当0<x<1时,r'(x)>0,故r(x)单调递增(如图),
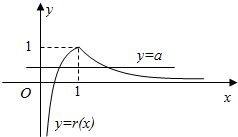
且$r(\frac{1}{e})=\frac{{-1+\frac{1}{e}}}{{\frac{1}{e^2}}}=-{e^2}+e<0$;
当x>1时,r'(x)<0,故r(x)单调递减,且$\frac{lnx+x}{x^2}>0$.
∴函数r(x)在x=1处取得最大值r(x)max=r(1)=1.
故要使$y=\frac{lnx+x}{x^2}$与y=a恰有两个不同的交点,只需0<a<1.
∴实数a的取值范围是(0,1).
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了恒成立问题的等价转化方法,考查了分类讨论的思想方法,考察了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
6.设集合A={x|$\frac{{x}^{2}}{2}$+y2=1},B={y|y=x2-1},则A∩B=( )
| A. | [-1,$\sqrt{2}$] | B. | {(-$\frac{\sqrt{6}}{2}$,$\frac{1}{2}$),($\frac{\sqrt{6}}{2}$,$\frac{1}{2}$)} | ||
| C. | {(-$\frac{\sqrt{6}}{2}$,$\frac{1}{2}$),($\frac{\sqrt{6}}{2}$,$\frac{1}{2}$),(0,1)} | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
10.cos(-2014π)的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | -$\frac{\sqrt{3}}{2}$ | D. | 0 |
12.函数f(x)=log2(x2+5x-6)的定义域是( )
| A. | [-2,3] | B. | (-6,1] | C. | (-∞,-1)∪(6,+∞) | D. | (-∞,-6)∪(1,+∞) |
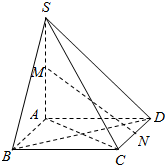 如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥平面ABCD,M,N分别为SA,CD的中点.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥平面ABCD,M,N分别为SA,CD的中点.