题目内容
【题目】已知函数![]() ,
,![]() .
.
(l)求![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 内存在唯一的极值点,求
内存在唯一的极值点,求![]() 的值.
的值.
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(2)
.(2)![]() 或
或![]() .
.
【解析】试题分析:(1)先求得函数定义域为![]() ,再利用函数的导数来求函数的单调区间。(2)即
,再利用函数的导数来求函数的单调区间。(2)即![]() 在区间
在区间![]() 上存在唯一零点,且为奇次零点。所以对函数g(x)求导
上存在唯一零点,且为奇次零点。所以对函数g(x)求导![]()
![]() .由(1)可知函数
.由(1)可知函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.而
上单调递减.而![]() ,所以g(x)最多两个零点,分别位于(0,1)和
,所以g(x)最多两个零点,分别位于(0,1)和![]() ,所以现在只需在(0,1)和
,所以现在只需在(0,1)和![]() 中各找一个
中各找一个![]() ,
,![]() ,使得
,使得![]() ,可找
,可找![]() <0,
<0,![]() ,所以一定有两个零点,因为要找的区间长度为1,所以再找
,所以一定有两个零点,因为要找的区间长度为1,所以再找![]() ,可求得
,可求得![]() 或
或![]() .
.
试题解析:(1)由已知得![]() ,
,![]() .
.
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() .
.
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)因为![]()
![]()
![]() ,
,
则![]()
![]() .
.
由(1)可知,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
又因为![]() ,
,![]() .
.
所以![]() 在
在![]() 上有且只有一个零点
上有且只有一个零点![]() .
.
又在![]() 上
上![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
在![]() 上
上![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() 为极值点,此时
为极值点,此时![]() .
.
又![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有且只有一个零点
上有且只有一个零点![]() .
.
又在![]() 上
上![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
在![]() 上
上![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
所以![]() 为极值点,此时
为极值点,此时![]() .
.
综上所述,![]() 或
或![]() .
.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
商店名称 | A | B | C | D | E |
销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
组别 | PM2.5浓度 | 频数(天) | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
(1)从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(2)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图. ①求图中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.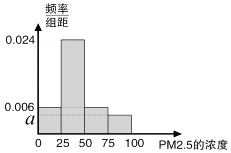
【题目】为了了解初三女生身高情况,某中学对初三女生身高情况进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中m,n,M,N所表示的数分别是多少?
(2)画出频率分布直方图;
(3)全体女生中身高在哪组范围内的人数最多?