题目内容
【题目】已知数列{an}中，a1=1且an+1=an+2n+1，设数列{bn}满足bn=an﹣1，对任意正整数n不等式 
均成立，则实数m的取值范围为 ．
【答案】[ 
，+∞）
【解析】解：由an+1=an+2n+1，则an+1﹣an=2n+1， 则a2﹣a1=3，
a3﹣a2=5，
a4﹣a3=7，
…
an﹣an﹣1=2n﹣1，
以上各式相加：an﹣a1=3+5+7+…+2n﹣1= 
=n2﹣1，
an=n2﹣1+a1=n2 ，
当n=1时成立，
∴an=n2 ，
bn=an﹣1=n2﹣1=（n+1）（n﹣1），
当n≥2时，则 
= 
= 
（ 
﹣ 
），
+ 
+…+ = （1﹣ 
）+ （ ﹣ 
）+ （ ﹣ 
）+…+ （ 
﹣ 
）+ （ ﹣ ），
= （1+ ﹣ ﹣ ）＜ ，
由 
，则 
，
实数m的取值范围[ ，+∞），
所以答案是：[ ，+∞）．
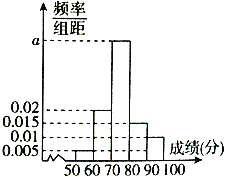
【题目】为了了解某学校高二年级学生的物理成绩，从中抽取n名学生的物理成绩（百分制）作为样本，按成绩分成 5组：[50，60），[60，70），[70，80），[80，90），[90，100]，频率分布直方图如图所示．成绩落在[70，80）中的人数为20．
男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
（Ⅰ）求a和n的值；
（Ⅱ）根据样本估计总体的思想，估计该校高二学生物理成绩的平均数
和中位数m；
（Ⅲ）成绩在80分以上（含80分）为优秀，样本中成绩落在[50，80）中的男、女生人数比为1：2，成绩落在[80，100]中的男、女生人数比为3：2，完成2×2列联表，并判断是否有95%的把握认为物理成绩优秀与性别有关．
参考公式和数据：K2=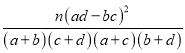
．
P（K2≥k） | 0.50 | 0.05 | 0.025 | 0.005 |
k | 0.455 | 3.841 | 5.024 | 7.879 |
