题目内容
已知无穷数列{an}的各项均为正整数,Sn为数列{an}的前n项和.
(1)若数列{an}是等差数列,且对任意正整数n都有Sn3=(Sn)3成立,求数列{an}的通项公式;
(2)对任意正整数n,从集合{a1,a2,…,an}中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与a1,a2,…,an一起恰好是1至Sn全体正整数组成的集合.
(ⅰ)求a1,a2的值;
(ⅱ)求数列{an}的通项公式.
(1)an=1或an=2n-1(2)a1=1,a2=3,an=3n-1
【解析】(1)设无穷等差数列{an}的公差为d,因为Sn3=(Sn)3对任意正整数n都成立,所以分别取n=1,n=2时,则有:
因为数列{an}的各项均为正整数,所以d≥0.
可得a1=1,d=0或d=2.(4分)
当a1=1,d=0时,an=1,Sn3=(Sn)3成立;
当a1=1,d=2时,Sn=n2,所以Sn3=(Sn)3.
因此,共有2个无穷等差数列满足条件,通项公式为an=1或an=2n-1.(6分)
(2)(ⅰ)记An={1,2,…,Sn},显然a1=S1=1.(7分)
对于S2=a1+a2=1+a2,有A2={1,2,…,Sn}={1,a2,1+a2,|1-a2|}={1,2,3,4},
故1+a2=4,所以a2=3.(9分)
(ⅱ)由题意可知,集合{a1,a2,…,an}按上述规则,共产生Sn个正整数.(10分)
而集合{a1,a2,…,an,an+1}按上述规则产生的Sn+1个正整数中,除1,2,…,Sn这Sn个正整数外,还有an-1,an+1+i,|an+1-i|(i=1,2,…,Sn),共2Sn+1个数.
所以,Sn+1=Sn+(2Sn+1)=3Sn+1.(12分)
又Sn+1+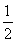 =3
=3 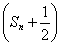 ,所以Sn=
,所以Sn=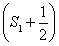 ·3n-1-
·3n-1-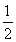 =
=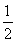 ·3n-
·3n-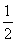 .(14分)
.(14分)
当n≥2时,an=Sn-Sn-1=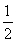 ·3n-
·3n-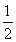 -
-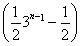 =3n-1.(15分)
=3n-1.(15分)
而a1=1也满足an=3n-1.
所以,数列{an}的通项公式是an=3n-1.(16分)

 科学实验活动册系列答案
科学实验活动册系列答案