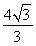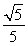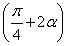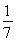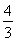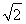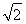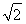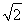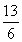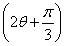题目内容
已知△ABC中，角A，B，C的对边分别为a，b，c，且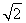
acos B＝ccos B＋bcos C.
(1)求角B的大小；
(2)设向量m＝(cos A，cos 2A)，n＝(12，－5)，求当m·n取最大值时，tan C的值．
（1）B＝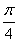
（2）7
【解析】(1)由题意，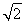
sin Acos B＝sin Ccos B＋cos Csin B，(2分)
所以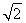
sin Acos B＝sin(B＋C)＝sin(π－A)＝sin A．(3分)
因为0＜A＜π，所以sin A≠0.
所以cos B＝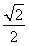
.(5分)
因为0＜B＜π，所以B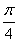＝.(6分)
(2)因为m·n＝12cos A－5cos 2A，(8分)
所以m·n＝－10cos2A＋12cos A＋5＝－10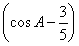
2＋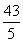
.(10分)
所以当cos A＝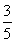
时，m·n取最大值．
此时sin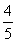 A＝
(0＜A＜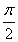
)，于是tan A＝
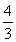.(12分)
所以tan C＝－tan(A＋B)＝－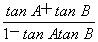
＝7.(14分)
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
