Question

已知数列{an}的前三项分别为a1＝5，a2＝6，a3＝8，且数列{an}的前n项和Sn满足Sn＋m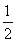＝(S2n＋S2m)－(n－m)2，其中m，n为任意正整数．

(1)求数列{an}的通项公式及前n项和Sn；

(2)求满足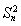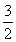－an＋33＝k2的所有正整数k，n.

 

Answer 1

（1）Sn＝n2＋3n＋1，n∈N*（2）n＝10，k＝131.

【解析】(1)在等式Sm＋n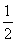＝(S2n＋S2m)－(n－m)2中，分别令m＝1，m＝2，得

Sn＋1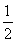＝(S2n＋S2)－(n－1)2，①

Sn＋2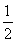＝ (S2n＋S4)－(n－2)2，②

②－①，得an＋2＝2n－3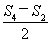＋.(3分)

在等式Sn＋m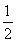＝(S2n＋S2m)－(n－m2)中，令n＝1，m＝2，得S3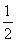＝(S2＋S4)－1，由题设知，S2＝11，S3＝19，故S4＝29.

所以an＋2＝2n＋6(n∈N*)，即an＝2n＋2(n≥3，n∈N*)．

又a2＝6也适合上式，故an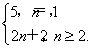＝ (5分)

Sn＝即Sn＝n2＋3n＋1，n∈N*.(6分)

(2)记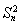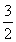－an＋33＝k2(*)．

n＝1时，无正整数k满足等式(*)．

n≥2时，等式(*)即为(n2＋3n＋1)2－3(n－10)＝k2.(8分)

①当n＝10时，k＝131.(9分)

②当n＞10时，则k＜n2＋3n＋1，

又k2－(n2＋3n)2＝2n2＋3n＋31＞0，所以k＞n2＋3n.

从而n2＋3n＜k＜n2＋3n＋1.

又因为n，k∈N*，所以k不存在，从而无正整数k满足等式(*)．(12分)

③当n＜10时，则k＞n2＋3n＋1，因为k∈N*，所以k≥n2＋3n＋2.

从而(n2＋3n＋1)2－3(n－10)≥(n2＋3n＋2)2.

即2n2＋9n－27≤0.因为n∈N*，所以n＝1或2.(14分)

n＝1时，k2＝52，无正整数解；

n＝2时，k2＝145，无正整数解．

综上所述，满足等式(*)的n，k分别为n＝10，k＝131.(16分)