��Ŀ����
̽������ ,x��(0,+��)����Сֵ����ȷ����Ӧ��x��ֵ���б����£�
,x��(0,+��)����Сֵ����ȷ����Ӧ��x��ֵ���б����£�
��۲����yֵ��xֵ�仯���ص㣬����������⣺
(1)������ ,(x>0)������(0,2)�ϵݼ������� �ϵ�����
,(x>0)������(0,2)�ϵݼ������� �ϵ�����
(2)��x= ʱ�� ,(x>0)����СֵΪ ��
,(x>0)����СֵΪ ��
(3)���ö���֤�� ,(x>0)������(0,2)�ϵݼ���
,(x>0)������(0,2)�ϵݼ���
(4)���� ,(x<0)����ֵ�������ֵ������Сֵ����ʱxΪ��ֵ��
,(x<0)����ֵ�������ֵ������Сֵ����ʱxΪ��ֵ��
��5���ⲻ��ʽ .
.
����˵����(1)(2)����Ľ��ֱ����д�ں����ϣ�(4)��ֱ�ӻش𣬲���֤����
 ,x��(0,+��)����Сֵ����ȷ����Ӧ��x��ֵ���б����£�
,x��(0,+��)����Сֵ����ȷ����Ӧ��x��ֵ���б����£�| x | �� | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | �� |
| y | �� | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | �� |
(1)������
 ,(x>0)������(0,2)�ϵݼ������� �ϵ�����
,(x>0)������(0,2)�ϵݼ������� �ϵ�����(2)��x= ʱ��
 ,(x>0)����СֵΪ ��
,(x>0)����СֵΪ ��(3)���ö���֤��
 ,(x>0)������(0,2)�ϵݼ���
,(x>0)������(0,2)�ϵݼ���(4)����
 ,(x<0)����ֵ�������ֵ������Сֵ����ʱxΪ��ֵ��
,(x<0)����ֵ�������ֵ������Сֵ����ʱxΪ��ֵ����5���ⲻ��ʽ
 .
.����˵����(1)(2)����Ľ��ֱ����д�ں����ϣ�(4)��ֱ�ӻش𣬲���֤����
(1)�� (2) )x=2ʱ��ymin="4 " (3)�� (4)���ֵ-4�� x=" -2" ��5����-5��-1��
(1) (2,+��) (��˵���Ա�) ��������������2��
(2)x=2ʱ��ymin="4" ��������������4��
(3) ��0<x1<x2<2����
f(x1)- f(x2)=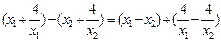
=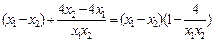 (#)����6/
(#)����6/
��0<x1<x2<2 ��x1-x2<0,0<x1x2<4 ��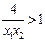 ��
��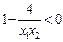
��f(x1)- f(x2)>0 ��f(x1)> f(x2)
��f(x)������(0,2)�ϵݼ� ��������������10��
(4) �����ֵ-4����ʱx=" -2" ��������������12��
��5����Ϊ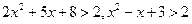
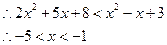 ���Խ⼯Ϊ��-5��-1�� ��������������16��
���Խ⼯Ϊ��-5��-1�� ��������������16��
(2)x=2ʱ��ymin="4" ��������������4��
(3) ��0<x1<x2<2����
f(x1)- f(x2)=
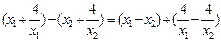
=
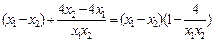 (#)����6/
(#)����6/��0<x1<x2<2 ��x1-x2<0,0<x1x2<4 ��
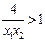 ��
��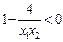
��f(x1)- f(x2)>0 ��f(x1)> f(x2)
��f(x)������(0,2)�ϵݼ� ��������������10��
(4) �����ֵ-4����ʱx=" -2" ��������������12��
��5����Ϊ
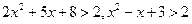
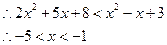 ���Խ⼯Ϊ��-5��-1�� ��������������16��
���Խ⼯Ϊ��-5��-1�� ��������������16��
��ϰ��ϵ�д�
�����Ŀ
 (x ��
(x �� )
) ,��m�ļ���M .
,��m�ļ���M .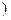 �ϵ�����������b��ȡֵ��Χ��_________.
�ϵ�����������b��ȡֵ��Χ��_________.  ������
������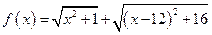 ����СֵΪ .
����СֵΪ .
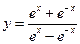 ��ͼ�����Ϊ�� ��
��ͼ�����Ϊ�� ��
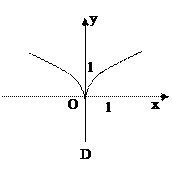
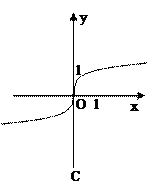
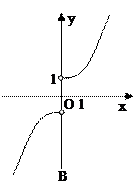

 ��ֵ��
��ֵ��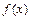 ��R�ϵ�������������
��R�ϵ�������������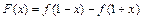 ����
����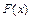 ��R�ϵ�
��R�ϵ�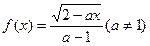 ��
��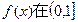 ���Ǽ���������ʵ��a��ȡֵ��Χ��
���Ǽ���������ʵ��a��ȡֵ��Χ��