题目内容
已知两条直线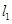 :y="m" 和
:y="m" 和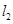 : y=
: y=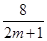 (m>0),
(m>0),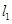 与函数
与函数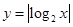 的图像从左至右相交于点A,B ,
的图像从左至右相交于点A,B ,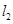 与函数
与函数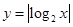 的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a ,b ,当m 变化时,
的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a ,b ,当m 变化时,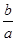 的最小值为
的最小值为
A.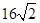 B.
B.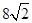 C.
C.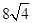 D.
D.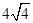
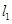 :y="m" 和
:y="m" 和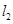 : y=
: y=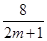 (m>0),
(m>0),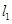 与函数
与函数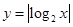 的图像从左至右相交于点A,B ,
的图像从左至右相交于点A,B ,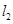 与函数
与函数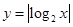 的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a ,b ,当m 变化时,
的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a ,b ,当m 变化时,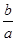 的最小值为
的最小值为A.
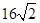 B.
B.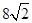 C.
C.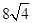 D.
D.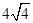
B
试题分析:设A,B,C,D各点的横坐标分别为xA,xB,xC,xD,依题意可求得为xA,xB,xC,xD的值,a=|xA﹣xC|,b=|xB﹣xD|,利用基本不等式可求得当m变化时,
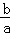 的最小值. 解:设A,B,C,D各点的横坐标分别为xA,xB,xC,xD,则﹣log2xA=m,log2xB=m;﹣log2xC=
的最小值. 解:设A,B,C,D各点的横坐标分别为xA,xB,xC,xD,则﹣log2xA=m,log2xB=m;﹣log2xC=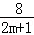 ,log2xD=
,log2xD=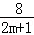 ;
;∴xA=2﹣m,xB=2m,xC=
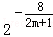 ,xD=
,xD=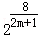 .
.∴a=|xA﹣xC|,b=|xB﹣xD|,
∴
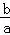 =
=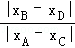 =|
=| |=2m•
|=2m•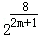 =
=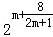 .
.又m>0,∴m+
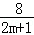 =
=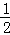 (2m+1)+
(2m+1)+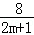 ﹣
﹣ ≥2
≥2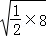 ﹣
﹣ =
=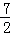 (当且仅当m=
(当且仅当m=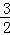 时取“=”)∴
时取“=”)∴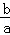 ≥
≥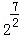 =8
=8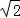 .
.故选B.
点评:本题考查对数函数图象与性质的综合应用,理解平行投影的概念,得到
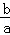 =
=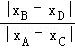 是关键,考查转化与数形结合的思想,考查分析与运算能力,属于难题
是关键,考查转化与数形结合的思想,考查分析与运算能力,属于难题
练习册系列答案
相关题目
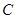 :
: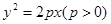 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.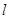 与抛物线
与抛物线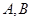 ,若满足
,若满足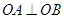 ,证明直线
,证明直线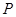 的坐标.
的坐标.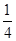



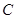 的极坐标方程为
的极坐标方程为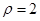 ,以极点为直角坐标系的原点,极轴为
,以极点为直角坐标系的原点,极轴为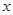 轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆
轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆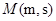 作平行于
作平行于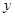 轴的直线
轴的直线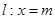 ,设
,设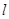 与
与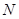 ,向量
,向量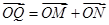 .
.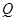 的轨迹方程;
的轨迹方程;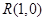 ,求
,求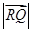 的最小值.
的最小值.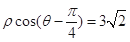 ,曲线
,曲线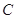 :
: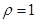 上的点到直线的距离为
上的点到直线的距离为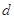 ,则
,则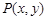 在椭圆
在椭圆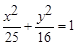 上,若
上,若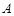 点坐标为
点坐标为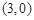 ,
,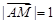 ,且
,且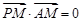 ,则
,则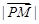 的最小值是( )
的最小值是( )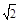
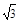
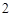

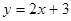 与抛物线
与抛物线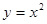 所围成的图形面积是( )
所围成的图形面积是( )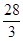
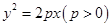 的准线经过椭圆
的准线经过椭圆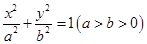 的左焦点,且经过抛物线与椭圆两个交点的弦过抛物线的焦点,则椭圆的离心率为_____________
的左焦点,且经过抛物线与椭圆两个交点的弦过抛物线的焦点,则椭圆的离心率为_____________