题目内容
直线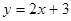 与抛物线
与抛物线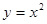 所围成的图形面积是( )
所围成的图形面积是( )
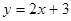 与抛物线
与抛物线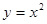 所围成的图形面积是( )
所围成的图形面积是( )| A.20 | B.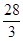 | C.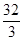 | D.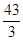 |
C
试题分析:由定积分的几何意义,直线
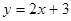 与抛物线
与抛物线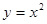 所围成的图形面积是
所围成的图形面积是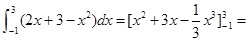
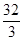 ,故选C。
,故选C。点评:简单题,利用定积分的几何意义,将面积计算问题转化成定积分计算。

练习册系列答案
相关题目
题目内容
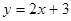 与抛物线
与抛物线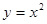 所围成的图形面积是( )
所围成的图形面积是( )| A.20 | B.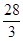 | C.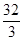 | D.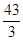 |
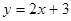 与抛物线
与抛物线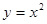 所围成的图形面积是
所围成的图形面积是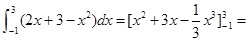
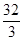 ,故选C。
,故选C。