题目内容
11．
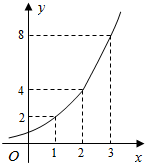如图所示的是某海域浒苔蔓延的面积（m2）与时间x（天）的满足函数关系y=ax，有以下叙述：①这个指数函数的底数是2；
②第6天的浒苔的面积就会超过60m2；
③浒苔每天增加的面积都相等；
④若浒苔蔓延到20m2，30m2，600m2所经过的时间分别为x1，x2，x3，则x1+x2=x3．
以上结论正确的是（ ）
| A． | ①② | B． | ①②④ | C． | ①②③ | D． | ②③④ |
分析 把点（1，2）代入函数解析式求出a值判断①；在函数解析式中取x=6求出y值判断②；直接由图象判断③；利用对数的运算性质求解得到x1+x2=x3判断④．
解答 解：①∵点（1，2）在函数图象上，
∴2=a1，∴a=2，故①正确；
②函数y=2x在R上是增函数，且当x=6时，y=64，故②正确；
③如图所示，1-2天增加2m2，2-3天增加4m2，故③不正确；
④由于：$20={2}^{{x}_{1}}，30={2}^{{x}_{2}}，600={2}^{{x}_{3}}$，
∴x1=log220，x2=log230，x3=log2600，
又∵log220+log230=log220×30=log2600，
∴若浮萍蔓延到20m2、30m2、600m2所经过的时间分别为x1，x2，x3，则x1+x2=x3成立，故④正确．
故选：B．
点评 本题考查的是函数模型的选择和应用问题、数形结合法．在解答的过程当中充分体现了观察图形、分析图形和利用图形的能力，同时对对数的运算能力也得到了体现，
是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．抽取某种型号的车床生产的10个零件，编号为A1，A2，…，A10，测量其直径（单位：cm），得到下面数据：
其中直径在区间[1.49，1.51]内的零件为一等品．
（1）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；
（2）从一等品零件中，随机抽取2个．
①用零件的编号列出所有可能的抽取结果；
②求这2个零件直径相等的概率；
（3）若甲、乙分别从一等品中各取一个，求甲取到零件的直径大于乙取到零件的直径的概率．
| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 直径 | 1.51 | 1.49 | 1.49 | 1.51 | 1.49 | 1.48 | 1.47 | 1.53 | 1.52 | 1.47 |
（1）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；
（2）从一等品零件中，随机抽取2个．
①用零件的编号列出所有可能的抽取结果；
②求这2个零件直径相等的概率；
（3）若甲、乙分别从一等品中各取一个，求甲取到零件的直径大于乙取到零件的直径的概率．
16．设a，b是实数，则“ab＞0”是“a+b＞0”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件已知 |