题目内容
1．已知公差不为0的等差数列{an}，其前n项和为Sn，若a1，a3，a4成等比数列，则$\frac{{{S_3}-{S_2}}}{{{S_5}-{S_3}}}$的值为2．分析 由题意可得：a3=a1+2d，a4=a1+3d，结合a1、a3、a4成等比数列，得到a1=-4d，进而根据等差数列的通项公式化简所求的式子即可得出答案．
解答 解：设等差数列的公差为d（d≠0），首项为a1，
所以a3=a1+2d，a4=a1+3d，
因为a1、a3、a4成等比数列，
所以（a1+2d）2=a1（a1+3d），
解得：a1=-4d，
则$\frac{{{S_3}-{S_2}}}{{{S_5}-{S_3}}}$=$\frac{{S}_{3}-{S}_{2}}{{（S}_{5}-{S}_{4}）+（{S}_{4}-{S}_{3}）}$
=$\frac{{a}_{3}}{{a}_{5}+{a}_{4}}$=$\frac{{a}_{1}+2d}{2{a}_{1}+7d}$=$\frac{-4d+2d}{-8d+7d}$=2．
故答案为：2．
点评 解决此类问题的关键是熟练掌握等比数列与等差数列的性质，利用性质解决问题．
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
11．
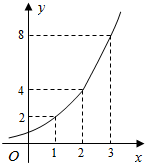如图所示的是某海域浒苔蔓延的面积（m2）与时间x（天）的满足函数关系y=ax，有以下叙述：
①这个指数函数的底数是2；
②第6天的浒苔的面积就会超过60m2；
③浒苔每天增加的面积都相等；
④若浒苔蔓延到20m2，30m2，600m2所经过的时间分别为x1，x2，x3，则x1+x2=x3．
以上结论正确的是（ ）
如图所示的是某海域浒苔蔓延的面积（m2）与时间x（天）的满足函数关系y=ax，有以下叙述：①这个指数函数的底数是2；
②第6天的浒苔的面积就会超过60m2；
③浒苔每天增加的面积都相等；
④若浒苔蔓延到20m2，30m2，600m2所经过的时间分别为x1，x2，x3，则x1+x2=x3．
以上结论正确的是（ ）
| A． | ①② | B． | ①②④ | C． | ①②③ | D． | ②③④ |
16．下列四个命题，其中正确命题的个数（ ）
①若a＞|b|，则a2＞b2
②若a＞b，c＞d，则a-c＞b-d
③若a＞b，c＞d，则ac＞bd
④若a＞b＞o，则$\frac{c}{a}$＞$\frac{c}{b}$．
①若a＞|b|，则a2＞b2
②若a＞b，c＞d，则a-c＞b-d
③若a＞b，c＞d，则ac＞bd
④若a＞b＞o，则$\frac{c}{a}$＞$\frac{c}{b}$．
| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
6．对任意$x∈（{0，\frac{π}{2}}）$，不等式sinx•f（x）＜cosx•f′（x）恒成立，则下列不等式错误的是（ ）
| A． | $f（{\frac{π}{3}}）＞\sqrt{2}f（{\frac{π}{4}}）$ | B． | $f（{\frac{π}{3}}）＞2cos1•f（1）$ | C． | $f（{\frac{π}{4}}）＜\sqrt{2}cos1•f（1）$ | D． | $f（{\frac{π}{4}}）＜\frac{{\sqrt{6}}}{2}f（{\frac{π}{6}}）$ |
13．设全集U={x|x＜4，x∈N}，A={0，1，2}，B={2，3}，则B∪∁UA等于（ ）
| A． | {3} | B． | {2，3} | C． | ∅ | D． | {0，1，2，3} |
11．下列命题是假命题的是（ ）
| A． | 若$\overrightarrow{a}•\overrightarrow{b}$=0（$\overrightarrow{a}$≠0，$\overrightarrow{b}$≠0），则$\overrightarrow{a}⊥\overrightarrow{b}$ | B． | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C． | 若ac2＞bc2，则a＞b | D． | 若α=60°，则cosα=$\frac{1}{2}$ |