题目内容
20.已知函数f(x)=x3-3x.(1)求函数f(x)的极值;
(2)过点P(1,n)(n≠-2)作曲线y=f(x)的切线,问:实数n满足什么样的取值范围,过点P可以作出三条切线?
分析 (1)求出f(x)的导数,求得单调区间,即可得到极值;
(2)求出导数,设出切点M(x0,y0),求得切线的斜率,以及切线的方程,代入点(1,n),可得过点(1,n)可作曲线的三条切线,即为关于x0方程$2x_0^3-3x_0^2+n+3$=0有三个实根.设g(x0)=$2x_0^3-3x_0^2+m+3$,求得导数,求得单调区间和极值,可令极大值大于0,极小值小于0,解不等式即可得到n的范围.
解答 解:(1)∵f'(x)=3x2-3=0,
由-1<x<1时,f′(x)<0,f(x)递减,
x>1或x<-1时,f′(x)>0,f(x)递增.
∴在x=±1处取得极值,
即有极大值f(-1)=2,极小值f(1)=-2;
(2)f′(x)=3x2-3=3(x+1)(x-1),
∵曲线方程为y=x3-3x,∴点P(1,n)不在曲线上.
设切点为M(x0,y0),则点M的坐标满足${y_0}=x_0^3-3x_0^{\;}$.
因$f'(x_0^{\;})=3(x_0^2-1)$,故切线的斜率为$3(x_0^2-1)=\frac{{x_0^3-3x_0^{\;}-n}}{{x_0^{\;}-1}}$,
整理得$2x_0^3-3x_0^2+n+3=0$.
∵过点P(1,n)可作曲线的三条切线,
∴关于x0方程$2x_0^3-3x_0^2+n+3$=0有三个实根.
设g(x0)=$2x_0^3-3x_0^2+m+3$,则g′(x0)=6$x_0^2-6x_0^{\;}$,
由g′(x0)=0,得x0=0或x0=1.
∴g(x0)在(-∞,0),(1,+∞)上单调递增,在(0,1)上单调递减.
∴函数g(x0)=$2x_0^3-3x_0^2+m+3$的极值点为x0=0,x0=1
∴关于x0方程$2x_0^3-3x_0^2+n+3$=0有三个实根的充要条件是$\left\{\begin{array}{l}g(0)>0\\ g(1)<0\end{array}\right.$,解得-3<n<-2.
故所求的实数a的取值范围是-3<n<-2.
点评 本题考查导数的运用:求切线的方程和单调区间、极值,考查函数方程的转化思想的运用,考查运算求解能力,属于中档题.

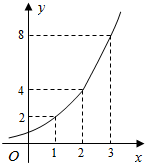 如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:
如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:①这个指数函数的底数是2;
②第6天的浒苔的面积就会超过60m2;
③浒苔每天增加的面积都相等;
④若浒苔蔓延到20m2,30m2,600m2所经过的时间分别为x1,x2,x3,则x1+x2=x3.
以上结论正确的是( )
| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ②③④ |
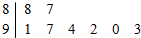 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91.5、5 | B. | 91、5 | C. | 92、5.5 | D. | 92、5 |
| A. | $\frac{3}{4}+\frac{1}{2π}$ | B. | $\frac{1}{4}-\frac{1}{2π}$ | C. | $\frac{1}{2}-\frac{1}{π}$ | D. | $\frac{1}{2}+\frac{1}{π}$ |