题目内容
3.求满足$\frac{1}{2}$<sinθ≤$\frac{\sqrt{3}}{2}$的θ的取值范围.分析 首先,计算正弦值分别为$\frac{1}{2}$和$\frac{\sqrt{3}}{2}$的角度,然后,结合正弦函数的单调性写出其取值范围即可.
解答 解:∵sin$\frac{π}{3}$=sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$,
sin$\frac{π}{6}$=sin$\frac{5π}{6}$=$\frac{1}{2}$,
∴θ的取值范围:
(2kπ+$\frac{π}{6}$,2kπ+$\frac{π}{3}$]∪[2kπ+$\frac{2π}{3}$,2kπ+$\frac{5π}{6}$),k∈Z.
点评 本题重点考查了正弦函数的单调性与单调区间等知识,属于中档题.

练习册系列答案
相关题目
11.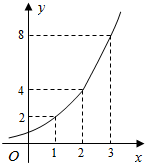 如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:
如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:
①这个指数函数的底数是2;
②第6天的浒苔的面积就会超过60m2;
③浒苔每天增加的面积都相等;
④若浒苔蔓延到20m2,30m2,600m2所经过的时间分别为x1,x2,x3,则x1+x2=x3.
以上结论正确的是( )
 如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:
如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:①这个指数函数的底数是2;
②第6天的浒苔的面积就会超过60m2;
③浒苔每天增加的面积都相等;
④若浒苔蔓延到20m2,30m2,600m2所经过的时间分别为x1,x2,x3,则x1+x2=x3.
以上结论正确的是( )
| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ②③④ |
8.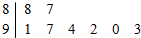 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
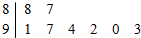 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91.5、5 | B. | 91、5 | C. | 92、5.5 | D. | 92、5 |
15.设复数z=(x-1)+yi(x∈R,y≥0),若|z|≤1,则y≥x的概率为( )
| A. | $\frac{3}{4}+\frac{1}{2π}$ | B. | $\frac{1}{4}-\frac{1}{2π}$ | C. | $\frac{1}{2}-\frac{1}{π}$ | D. | $\frac{1}{2}+\frac{1}{π}$ |
13.设全集U={x|x<4,x∈N},A={0,1,2},B={2,3},则B∪∁UA等于( )
| A. | {3} | B. | {2,3} | C. | ∅ | D. | {0,1,2,3} |
 定义运算?,a?b=S的运算原理如伪代码所示,则式子5?3+2?4=32.
定义运算?,a?b=S的运算原理如伪代码所示,则式子5?3+2?4=32.