题目内容
1.记函数f(x)=ax2+bx+c(a,b,c均为常数,且a≠0).(1)若a=1,f(b)=f(c)(b≠c),求f(2)的值;
(2)若b=1,c=-a时,函数y=f(x)在区间[1,2]上的最大值为g(a),求g(a).
分析 (1)将a=1代入,结合f(b)=f(c)(b≠c),可得2b+c=0,进而得到答案;
(2)将b=1,c=-a代入,分析函数的图象和性质,进行分类讨论不同情况下,函数y=f(x)在区间[1,2]上的最大值,综合讨论结果,可得答案.
解答 解:(1)当a=1时,f(x)=x2+bx+c,
由f(b)=f(c),可得b2+b2+c=c2+bc+c,
即2b2-bc-c2=0,(b-c)(2b+c)=0,解得b=c或2b+c=0,(2分)
∵b≠c,
∴2b+c=0,(4分)
所以f(2)=4+2b+c=4.(6分)
(2)当b=1,c=-a时,$f(x)=a{x^2}+x-a=a{({x+\frac{1}{2a}})^2}-a-\frac{1}{4a}$,x∈[1,2],(7分)
①当a>0时,$x=-\frac{1}{2a}<1$时,f(x)在区间[1,2]上单调递增,
所以fmax(x)=f(2)=3a+2; (9分)
②当a<0时,
Ⅰ.若$-\frac{1}{2a}≥2$,即$-\frac{1}{4}≤a<0$时,f(x)在区间[1,2]上单调递增,
所以fmax(x)=f(2)=3a+2; (11分)
Ⅱ.若$-\frac{1}{2a}≤1$,即$a≤-\frac{1}{2}$时,f(x)在区间[1,2]上单调递减,
所以fmax(x)=f(1)=1; (13分)
Ⅲ.若$1<-\frac{1}{2a}<2$,即$-\frac{1}{2}<a<-\frac{1}{4}$时,f(x)在区间$[{1,-\frac{1}{2a}}]$上单调递增,$[{-\frac{1}{2a},2}]$上单调递减,
所以${f_{max}}(x)=f({-\frac{1}{2a}})=-a-\frac{1}{4a}$.(15分)
综上可得:$g(a)=\left\{{\begin{array}{l}{3a+2,a≥-\frac{1}{4}且a≠0}\\{-a-\frac{1}{4a},-\frac{1}{2}<a<-\frac{1}{4}}\\{1,a≤-\frac{1}{2}}\end{array}}\right.$.(16分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.

| A. | ab>0,bc>0 | B. | ab>0,bc<0 | C. | ab<0,bc>0 | D. | ab<0,bc<0 |
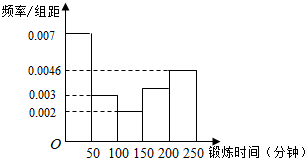 某个公司调查统计它的员工每周参与体育锻炼的时间,样本容量为100人,将调查结果统计为频率分布直方图,如图.我们将每周体育锻炼时间不低于150分钟的人称为“勤于锻炼者”,并将有关性别的信息统计到表中.
某个公司调查统计它的员工每周参与体育锻炼的时间,样本容量为100人,将调查结果统计为频率分布直方图,如图.我们将每周体育锻炼时间不低于150分钟的人称为“勤于锻炼者”,并将有关性别的信息统计到表中.| “勤于锻炼者” | 非“勤于锻炼者” | 合计 | |
| 男 | 25 | 70 | |
| 女 | |||
| 合计 |
附:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1}+{n}_{2}+{n}_{+1}+{n}_{+2}}$
| p(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(3)由于猜测员工的锻炼时间y与年龄x成线性相关,所以根据调查结果进行了线性回归分析,得到回归方程为y=-5x+b,如果员工的平均锻炼时间是110分钟,那么请判断下列说法的正误:
①b=285;
②由于回归方程的斜率是负的,说明年龄越大的员工,每周锻炼时间一定越短;
③由于回归直线方程的斜率是负的,说明两个变量的相关关系是负相关;
④能够算出回归方程,说明两个变旦之间确实是线性相关关系;
⑤回归直线是所有直线中穿过数据点最多的直线;
⑥两个变量是不是成线性相关关系还要看相关系数的大小.
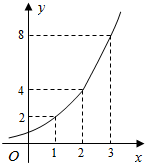 如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:
如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述: