题目内容
【题目】为了解某中学学生对《中华人民共和国交通安全法》的了解情况，调查部门在该校进行了一次问卷调查（共12道题），从该校学生中随机抽取40人，统计了每人答对的题数，将统计结果分成
，
，
，
，
，
六组，得到如下频率分布直方图.
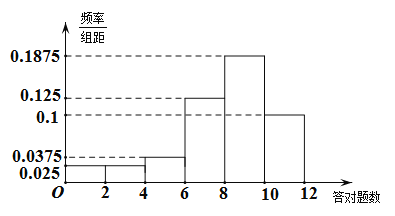
（1）估计这组数据的平均数（同一组中的数据用该组区间的中点值作代表）；
（2）若从答对题数在
内的学生中随机抽取2人，求恰有1人答对题数在内的概率.
【答案】（1）
；（2）
【解析】
（1）用每个长方形的面积
底边中点值，累加即为平均数的估计值；
（2）根据题意计算出在
内的学生人数，计算出所有答题的情况，再计算出满足题意的情况，用古典概型计算公式进行计算即可.
（1）估计平均数为：
.
（2）答对题数在
内的学生有
人，记为A，B；
答对题数在
内的学生有
人，记为c，d，e.
从答对题数在内的学生中随机抽取2人的情况有
，
，
，
，
，
，
，
，
，
，共10种，
恰有1人答对题数在内的情况有
，，，，，，共6种，
故所求概率
.
【题目】某工厂的机器上存在一种易损元件，这种元件发生损坏时，需要及时维修. 现有甲、乙两名工人同时从事这项工作，下表记录了某月1日到10日甲、乙两名工人分别维修这种元件的件数.
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 |
甲维修的元件数 | 3 | 5 | 4 | 6 | 4 | 6 | 3 | 7 | 8 | 4 |
乙维修的元件数 | 4 | 7 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 7 |
（1）从这
天中，随机选取一天，求甲维修的元件数不少于5件的概率；
（2）试比较这10天中甲维修的元件数的方差
与乙维修的元件数的方差
的大小.（只需写出结论）；
（3）由于甲、乙的任务量大，拟增加工人，为使增加工人后平均每人每天维修的元件不超过3件，请利用上表数据估计最少需要增加几名工人.
【题目】已知某企业有职工5000人，其中男职工3500人，女职工1500人．该企业为了丰富职工的业余生活，决定新建职工活动中心，为此，该企业工会采用分层抽样的方法，随机抽取了300名职工每周的平均运动时间（单位：h），汇总得到频率分布表（如表所示），并据此来估计该企业职工每周的运动时间：
平均运动时间 | 频数 | 频率 |
[0，2） | 15 | 0.05 |
[2，4） | m | 0.2 |
[4，6） | 45 | 0.15 |
[6，8） | 755 | 0.25 |
[8，10） | 90 | 0.3 |
[10，12） | p | n |
合计 | 300 | 1 |
（1）求抽取的女职工的人数；
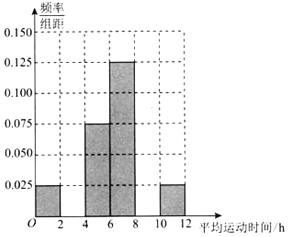
（2）①根据频率分布表，求出m、n、p的值，完成如图所示的频率分布直方图，并估计该企业职工每周的平均运动时间不低于4h的概率；
男职工 | 女职工 | 总计 | |
平均运动时间低于4h | |||
平均运动时间不低于4h | |||
总计 |
②若在样本数据中，有60名女职工每周的平均运动时间不低于4h，请完成以下2×2列联表，并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h与性别有关”．
附：K2=
，其中n=a+b+c+d．
P（K2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】“伟大的变革—庆祝改革开放
周年大型展览”于
年
月
日在中国国家博物馆闭幕，本次特展紧扣“改革开放年光辉历程”的主线，多角度、全景式描绘了我国改革开放年波澜壮阔的历史画卷．据统计，展览全程呈现出持续火爆的状态，现场观众累计达
万人次，参展人数屡次创造国家博物馆参观纪录，网上展馆点击浏览总量达
亿次．
下表是年
月参观人数（单位：万人）统计表
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
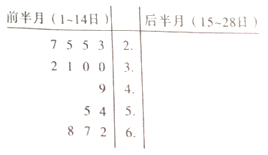
根据表中数据回答下列问题：
（1）请将年月前半月（
日）和后半月（
日）参观人数统计对比茎叶图填补完整，并通过茎叶图比较两组数据方差的大小（不要求计算出具体值，得出结论即可）；
（2）将年月参观人数数据用该天的对应日期作为样本编号，现从中抽样
天的样本数据．若抽取的样本编号是以
为公差的等差数列，且数列的第项为
，求抽出的这个样本数据的平均值；
（3）根据国博以往展览数据及调查统计信息可知，单日入馆参观人数为
（含，单位：万人）时，参观者的体验满意度最佳，在从
中抽出的样本数据中随机抽取三天的数据，参观者的体验满意度为最佳的天数记为
，求的分布列与期望．
