题目内容
【题目】若函数
为常数，
）的图象关于直线
对称，则函数
的图象（ ）
A. 关于直线
对称B. 关于直线对称
C. 关于点
对称D. 关于点
对称
【答案】D
【解析】
利用三角函数的对称性求得a的值，可得g（x）的解析式，再代入选项，利用正弦函数的图象的对称性，得出结论．
解：∵函数f（x）＝asinx+cosx（a为常数，x∈R）的图象关于直线x＝
对称，
∴f（0）＝f（
），即
，∴a＝
，
所以函数g（x）＝sinx+acosx＝sinx+cosx＝
sin（x+），
当x＝﹣时，g（x）＝-，不是最值，故g（x）的图象不关于直线x＝﹣对称，故A错误，
当x＝时，g（x）＝1，不是最值，故g（x）的图象不关于直线x＝对称，故B错误，
当x＝时，g（x）＝≠0，故C错误，
当x＝
时，g（x）＝0，故D正确，
故选：D．
练习册系列答案
相关题目
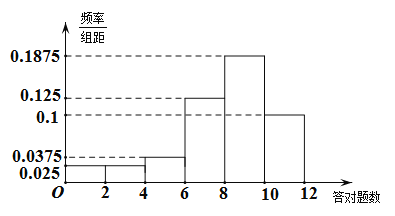
【题目】为了了解校园噪音情况，学校环保协会对校园噪音值（单位：分贝）进行了
天的监测，得到如下统计表：
噪音值（单位：分贝） |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
（1）根据该统计表，求这
天校园噪音值的样本平均数（同一组的数据用该组组间的中点值作代表）.
（2）根据国家声环境质量标准：“环境噪音值超过
分贝，视为重度噪音污染；环境噪音值不超过
分贝，视为度噪音污染.”如果把由上述统计表算得的频率视作概率，回答下列问题：
（i）求周一到周五的五天中恰有两天校园出现重度噪音污染而其余三天都是轻度噪音污染的概率.
（ii）学校要举行为期
天的“汉字听写大赛”校园选拔赛，把这
天校园出现的重度噪音污染天数记为
，求
的分布列和方差
.
