题目内容
1.已知向量$\overrightarrow{m}$=(cosx,-1),$\overrightarrow{n}$=($\sqrt{3}$sinx,cos2x),设函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$+$\frac{1}{2}$.(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)当x∈(0,$\frac{π}{2}$)时,求函数f(x)的值域.
分析 (Ⅰ)利用已知条件通过向量的数量积求出函数的解析式,求才函数的周期以及单调增区间.
(Ⅱ)利用角的范围,求出相位的范围,然后求出值域.
解答 解:(Ⅰ)依题意向量$\overrightarrow{m}$=(cosx,-1),$\overrightarrow{n}$=($\sqrt{3}$sinx,cos2x),
函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$+$\frac{1}{2}$=$\sqrt{3}sinxcosx-{cos}^{2}x$$+\frac{1}{2}$=$sin(2x-\frac{π}{6})$.
得$f(x)=sin(2x-\frac{π}{6})$…(3分)
∴f(x)的最小正周期是:T=π…(4分)
由$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}$解得$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3}$,k∈Z.
从而可得函数f(x)的单调递增区间是:$[kπ-\frac{π}{6},kπ+\frac{π}{3}],k∈Z$…(6分)
(Ⅱ)由$0<x<\frac{π}{2}$,可得$-\frac{π}{6}<2x-\frac{π}{6}<\frac{5π}{6}$…(9分)
从而可得函数f(x)的值域是:$(-\frac{1}{2},1]$…(12分)
点评 本题考查两角和与差的三角函数,向量的数量积的应用,三角函数的周期的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如果执行如图的程序框图,输出的结果为( )
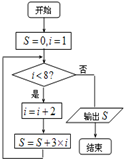

| A. | 43 | B. | 69 | C. | 72 | D. | 54 |
9.已知$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{{e}_{3}}$均为单位向量,其中任何两个向量的夹角均为120°,则|$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$+$\overrightarrow{{e}_{3}}$|=( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 0 |
6. 如图,平行四边形的顶点A位于双曲线的中心,顶点B位于该双曲线的右焦点,∠ABC为60°,顶点D恰在该双曲线的左支上,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,则此双曲线的离心率是( )
如图,平行四边形的顶点A位于双曲线的中心,顶点B位于该双曲线的右焦点,∠ABC为60°,顶点D恰在该双曲线的左支上,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,则此双曲线的离心率是( )
 如图,平行四边形的顶点A位于双曲线的中心,顶点B位于该双曲线的右焦点,∠ABC为60°,顶点D恰在该双曲线的左支上,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,则此双曲线的离心率是( )
如图,平行四边形的顶点A位于双曲线的中心,顶点B位于该双曲线的右焦点,∠ABC为60°,顶点D恰在该双曲线的左支上,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,则此双曲线的离心率是( )| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\frac{{\sqrt{7}+\sqrt{3}}}{2}$ | D. | $\frac{5}{2}$ |
13.在等差数列{an}中,a3+a5+a7=90,则2a6-a7等于( )
| A. | 30 | B. | 24 | C. | 20 | D. | 15 |
10.以抛物线y=$\frac{1}{4}$x2的焦点为圆心,且过坐标原点的圆的方程为( )
| A. | x2+y2-x=0 | B. | x2+y2-2x=0 | C. | x2+y2-y=0 | D. | x2+y2-2y=0 |