题目内容
【题目】如图,矩形![]() (
(![]() ),被截去一角(即
),被截去一角(即![]() ),
),![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.
(1)求五棱锥![]() 的体积的最大值;
的体积的最大值;
(2)在(1)的情况下,证明: ![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)过![]() 作
作![]() ,由面面垂直性质定理得
,由面面垂直性质定理得![]() 平面
平面![]() ,即为五棱锥
,即为五棱锥![]() 的高,再利用平几知识计算底面面积,由
的高,再利用平几知识计算底面面积,由![]() 得
得![]() 在以
在以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆上,由椭圆的简单的几何性质知:点
的椭圆上,由椭圆的简单的几何性质知:点![]() 为短轴端点时,
为短轴端点时, ![]() 到
到![]() 的距离最大,最后代入锥体体积公式即可,(2)过
的距离最大,最后代入锥体体积公式即可,(2)过![]() 作
作![]() ,由面面垂直性质定理得
,由面面垂直性质定理得![]() 平面
平面![]() ,即得
,即得![]() ,再在平面
,再在平面![]() 内,根据平几知识计算可得
内,根据平几知识计算可得![]() .最后根据线面垂直判定定理得
.最后根据线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() .
.
试题解析:(Ⅰ)解:因为![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
所以截去的![]() 是等腰直角三角形,
是等腰直角三角形,
所以![]() .
.
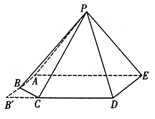
如图3,
过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
, ![]() 为五棱锥
为五棱锥![]() 的高.
的高.
在平面![]() 内,
内, ![]() ,
, ![]() 在以
在以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆上,
的椭圆上,
由椭圆的简单的几何性质知:点![]() 为短轴端点时,
为短轴端点时, ![]() 到
到![]() 的距离最大,
的距离最大,
此时![]() ,
, ![]() ,(指出即可,未说明理由不扣分)
,(指出即可,未说明理由不扣分)
所以![]() ,
,
所以![]() .
.
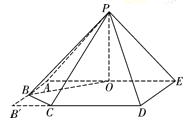
(Ⅱ)证明:连接![]() ,如图,据(Ⅰ)知,
,如图,据(Ⅰ)知, ![]() ,故
,故![]() 是等腰直角三角形,所以
是等腰直角三角形,所以![]() ,
,
所以![]() ,即
,即![]() .
.
由于![]() 平面
平面![]() ,所以
,所以![]() ,
,
而![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目