题目内容
20.已知数列{xn}满足x1=$\frac{1}{2}$,且xn+1=$\frac{{x}_{n}}{2-{x}_{n}}$,(n∈N+).设an=$\frac{1}{{x}_{n}}$,求前四项,归纳求数列{an}的通项公式.分析 由已知求出数列{an}的前4项,然后利用不完全归纳法归纳得到数列{an}的通项公式.
解答 解:由x1=$\frac{1}{2}$,且xn+1=$\frac{{x}_{n}}{2-{x}_{n}}$,
得${x}_{2}=\frac{{x}_{1}}{2-{x}_{1}}=\frac{\frac{1}{2}}{2-\frac{1}{2}}=\frac{1}{3}$,
${x}_{3}=\frac{{x}_{2}}{2-{x}_{2}}=\frac{\frac{1}{3}}{2-\frac{1}{3}}=\frac{1}{5}$,
${x}_{4}=\frac{{x}_{3}}{2-{x}_{3}}=\frac{\frac{1}{5}}{2-\frac{1}{5}}=\frac{1}{9}$,
∴${a}_{1}=\frac{1}{{x}_{1}}=\frac{1}{\frac{1}{2}}=2$=21-1+1,${a}_{2}=\frac{1}{{x}_{2}}=\frac{1}{\frac{1}{3}}=3$=22-1+1,${a}_{3}=\frac{1}{{x}_{3}}=\frac{1}{\frac{1}{5}}=5$=23-1+1,${a}_{4}=\frac{1}{{x}_{4}}=\frac{1}{\frac{1}{9}}=9$=24-1+1.
由上归纳可得:${a}_{n}={2}^{n-1}+1$.
点评 本题考查根据递推关系求数列的通项公式的方法,考查不完全归纳法,属中档题.

练习册系列答案
相关题目
11.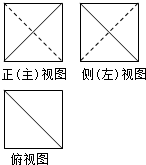 一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )
一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )
 一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )
一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 6 | D. | $\frac{20}{3}$ |
12.下列表示正确的是( )
| A. | {-2.5}∉Z | B. | ∅⊆{x|x<-3} | C. | {a}∈{a、b、c} | D. | 1⊆{1} |
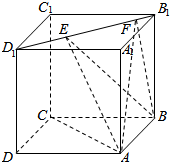 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,