如图.正方体ABCD-A1B1C1D1的棱长为1.线段B1D1上有两个动点E.F.且EF=$\frac{\sqrt{2}}{2}$.给出下列五个命题:①EF∥平面ABCD ②AC⊥BE③点A1到平面B1BDD1的距离为$\sqrt{2}$④三棱锥A-BEF的体积为定值.⑤异面直线AE.BF所成的角为定值其中真命题的序号是①.②.④．题目和参考答案——青夏教育精英家教网—

题目内容

10．

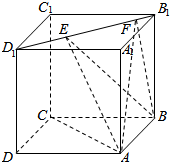如图，正方体ABCD-A₁B₁C₁D₁的棱长为1，线段B₁D₁上有两个动点E，F，且EF=$\frac{\sqrt{2}}{2}$，
给出下列五个命题：
①EF∥平面ABCD
②AC⊥BE
③点A₁到平面B₁BDD₁的距离为$\sqrt{2}$
④三棱锥A-BEF的体积为定值，⑤异面直线AE，BF所成的角为定值
其中真命题的序号是①，②，④．

分析此题考察空间几何体的线面问题，体积问题，和线线问题．需要学生的耐心分析，灵活转换，取特例等思想．

解答解：①由正方体ABCD-A₁B₁C₁D₁的两个底面平行，EF在其一面上，故EF与平面ABCD无公共点，故有EF∥平面ABCD，真命题；
②由题意及图形知，AC⊥面DD₁B₁B，故可得出AC⊥BE，真命题；
③A₁到平面B₁BDD₁的距离为A₁到B₁D₁的距离即$\frac{\sqrt{2}}{2}$．假命题；
④由几何体的性质及图形知，三角形BEF的面积是定值，A点到面DD₁B₁B距离等于点A₁到平面B₁BDD₁的距离是定值，故可得三棱锥A-BEF的体积为定值，真命题；
⑤取特例：由图知，当F与B1重合时，令上底面顶点为O，则此时两异面直线所成的角是∠A₁AO，当E与D₁重合时，此时点F与O重合，则两异面直线所成的角是OBC₁，此二角不相等，故异面直线AE、BF所成的角不为定值．假命题．
故答案为①，②，④

点评次题考察知识点比较多，对图形的考察比较抽象，学生应结合图形，根据概念耐心分析．

练习册系列答案

1．（重点中学做）为了考察某种药物预防疾病的效果，选用小白鼠进行动物实验，得到如下的2×2列联表：

	患病	未患病	总计
服用药	10	a₁	55
未服用药	a₂	30	a₄
总计	30	a₃	105

（1）求2×2列联表中a₁，a₂，a₃，a₄的值，并用独立性检验的思想方法分析：能有多大把握认为药物有效？说明理由：
（2）若按分层抽样的方法从未患病的小白鼠中抽取5只分批做进一步的实验，第一批实验从已选取的5只中任选两只，求第一批实验中至少有一只是服用了药物的动物的概率．
附：x²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$

p（x²≥k）	0.05	0.01	0.001
k	3.841	6.635	10.828

18．有下列几个命题：
①函数y=|x|（x∈{-2，-1，0，1，2，3}）的值域为{y|y≥0}；
②函数y=x²（x∈R且 x≠2）的值域为{y|y≥0，且y≠4}；
③函数y=$\sqrt{x-1}$的值域为{y|y≥0}． ④函数y=$\frac{{x}^{2}-1}{x-1}$的值域为R；
其中正确命题的序号为③．

5．在平面直角坐标系xoy中，以原点为极点，x轴的正半轴为极轴建立极坐标系．
（1）设曲线C的参数方程为$\left\{\begin{array}{l}{x=t}\\{y={t}^{2}}\end{array}\right.$（t为参数），求曲线C的极坐标方程；
（2）若l：$\left\{\begin{array}{l}{x=t}\\{y=t-a}\end{array}\right.$（t为参数）过椭圆C：$\left\{\begin{array}{l}{x=3cosφ}\\{y=2sinφ}\end{array}\right.$（φ为参数）的右顶点，求a的值．

15．函数y=x+$\frac{4}{x}$的值域为（-∞，-4]∪[4，+∞）．

2．下列命题中正确的是（　　）

	A．	若p⇒q，则q是p的充分条件
	B．	“若a＞b，则2^a＞2^b”的否命题为“若a＜b，则2^a＜2^b”
	C．	“?x∈R，x²+x≤1”的否定是“?x∈R，x²+x≥1”
	D．	“x＞0”是“x+$\frac{1}{x}$≥2”的充要条件

19．已知关于x的不等式ax²+bx+c＞0的解为x＜-1，或x＞3，试解关于x的不等式cx²-bx+a＞0．

20．已知集合A={x|x=a+b$\sqrt{2}$，a∈Z，b∈Z}，则$\frac{1}{\sqrt{2}-1}$∈A（填“∈”或“∉”）

试题分类