题目内容
11.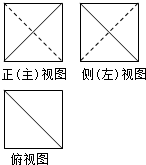 一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )
一个边长为2的正方体截去两个角后所得几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 6 | D. | $\frac{20}{3}$ |
分析 由已知中的三视图可得:该几何体是棱长为1的正方体截去两个角所得的组合体,画出其直观图,并求出截去部分的体积,相减可得答案.
解答 解:由已知中的三视图可得:该几何体是棱长为2的正方体截去两个角所得的组合体,
其直观图如下图所示: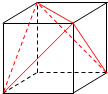
故组合体的体积V=2×2×2-2×($\frac{1}{3}$×$\frac{1}{2}$×2×2×2)=$\frac{16}{3}$,
故选:B.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
19.已知三次函数f(x)=(x-1)(x-2)(x-a)(1<a<2),则$\frac{1}{f′(1)}$+$\frac{4}{f′(2)}$+$\frac{{a}^{2}}{f′(a)}$=1.
1.(重点中学做)为了考察某种药物预防疾病的效果,选用小白鼠进行动物实验,得到如下的2×2列联表:
(1)求2×2列联表中a1,a2,a3,a4的值,并用独立性检验的思想方法分析:能有多大把握认为药物有效?说明理由:
(2)若按分层抽样的方法从未患病的小白鼠中抽取5只分批做进一步的实验,第一批实验从已选取的5只中任选两只,求第一批实验中至少有一只是服用了药物的动物的概率.
附:x2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 患病 | 未患病 | 总计 | |
| 服用药 | 10 | a1 | 55 |
| 未服用药 | a2 | 30 | a4 |
| 总计 | 30 | a3 | 105 |
(2)若按分层抽样的方法从未患病的小白鼠中抽取5只分批做进一步的实验,第一批实验从已选取的5只中任选两只,求第一批实验中至少有一只是服用了药物的动物的概率.
附:x2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| p(x2≥k) | 0.05 | 0.01 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |