题目内容
已知等差数列{an}中,a2+a4=10,a7=13,等比数列{bn}的公比q小于1,且b1,b2是方程27x2-12x+1=0的两根.
(1)求数列{an},{bn}的通项公式;
(2)求数列{an•bn}的前n项和Tn.
(1)求数列{an},{bn}的通项公式;
(2)求数列{an•bn}的前n项和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)利用已知条件直接求出等差数列和等比数列的通项公式.
(利用(1)的结论,使用乘公比错位相减法求得数列的和.
(利用(1)的结论,使用乘公比错位相减法求得数列的和.
解答:
解:(1)已知等差数列{an}中,a2+a4=10,a7=13,
则:
解得:an=2n-1
等比数列{bn}的公比q小于1,且b1,b2是方程27x2-12x+1=0的两根,
所以:
解得:bn=(
)n
(2)由(1)得:
cn=anbn=(2n-1)(
)n
Tn=c1+c2+…+cn=1•
+3•(
)2+…+(2n-3)(
)n-1+(2n-1)(
)n①
Tn=1•(
)2+3•(
)3+…+(2n-1)•(
)n+1②
①-②得:Tn=
[1-(
)n]-
-
(2n-1)(
)n+1]=-(n-1)(
)n+1
则:
|
解得:an=2n-1
等比数列{bn}的公比q小于1,且b1,b2是方程27x2-12x+1=0的两根,
所以:
|
解得:bn=(
| 1 |
| 3 |
(2)由(1)得:
cn=anbn=(2n-1)(
| 1 |
| 3 |
Tn=c1+c2+…+cn=1•
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
①-②得:Tn=
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查的知识要点:等差,等比数列的通项公式的求法,利用乘公比错位相减法求数列的和.属于基础题型.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
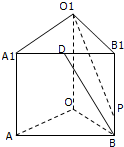 已知在直三棱柱ABO-A1B1O1中,OO1=4,OA=4,OB=3,∠AOB=90°,点D是线段A1B1的中点,点P是侧棱BB1上一点,若O1P与平面AOB所成的角正切值为
已知在直三棱柱ABO-A1B1O1中,OO1=4,OA=4,OB=3,∠AOB=90°,点D是线段A1B1的中点,点P是侧棱BB1上一点,若O1P与平面AOB所成的角正切值为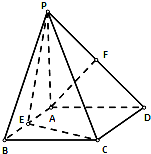 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.