题目内容
已知|
|=13，|
|=19，|
+
|=24，则|
-
|= ．
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：通过已知结合向量的平方等于模的平方，只要求出
，
的数量积即可．
| a |
| b |
解答：
解：已知|
|=13，|
|=19，|
+
|=24，
所以|
+
|2=242，所以132+192+2
•
=242，所以2
•
=242-192-132，
|
-
|2=|
|2+|
|2-2
•
=132+192-（242-192-132）=315，
所以|
-
|=3
．
| a |
| b |
| a |
| b |
所以|
| a |
| b |
| a |
| b |
| a |
| b |
|
| a |
| b |
| a |
| b |
| a |
| b |
所以|
| a |
| b |
| 35 |
点评：本题考查了向量的完全平方式与向量数量积的运算，考查了向量的平方等于向量模的平方，属于基础题．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
已知集合M={x|y=-
}，集合N={y|y=ex，x∈R}（e是自然对数的底数），则M∩N=（ ）
| 1-x |
| A、{x|0＜x≤1} |
| B、{x|0＜x＜1} |
| C、{x|0＜x＜1} |
| D、∅ |
若tanα=lg（10a），tanβ=lg（
），且α+β=
，则实数a的值为（ ）
| 1 |
| a |
| π |
| 4 |
| A、1 | ||
B、
| ||
C、1或
| ||
| D、1或10 |
设双曲线的一个焦点为F，虚轴的一个端点为B，如果直线FB与该双曲线的一条渐近线垂直，那么此双曲线的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
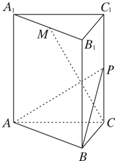如图，三棱柱ABC-A1B1C1的底面是边长为4正三角形，AA1⊥平面ABC，AA1=2
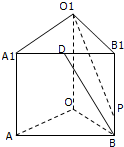已知在直三棱柱ABO-A1B1O1中，OO1=4，OA=4，OB=3，∠AOB=90°，点D是线段A1B1的中点，点P是侧棱BB1上一点，若O1P与平面AOB所成的角正切值为