题目内容

将正方形ABCD沿对角线折成直二面角，则二面角A-BC-D的平面角的余弦值是
 
．
考点：二面角的平面角及求法
专题：空间角
分析：取BC的中点E，作OF⊥BC，可得∠AEO为二面角A-BC-D的平面角，求出三角形的三边，即可得到结论．
解答： 解：取BC的中点E，OF⊥BC，可得∠AEO为二面角A-BC-D的平面角
设正方形ABCD的边长为1，
∴A0=
2
2
，OE=
1
2
CD=
1
2
，
则AE=
(
1
2
)2+(
2
2
)2
=
3
2
，
则cos∠AEO=
OE
AE
=
1
2
3
2
=
3
3
，
故答案为：
3
3
点评：本题考查图形的翻折，考查面面角，考查余弦定理的运用，正确作出面面角是关键．
练习册系列答案
相关题目
计算：8
2
3
=
 
．
在椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）中，F1、F2分别是其左右焦点，若椭圆上存在点P使得|PF1|-2|PF2|=a，则该椭圆的离心率的取值范围是（　　）
A、（
2
3
，1）
B、（0，
2
3
]
C、[
1
3
，1）
D、[
2
3
，1）
设
a
、
b
不共线，
c
=2
a
-
b
，
d
=3
a
-2
b
，试判断
c
、
d
能否作为基底．
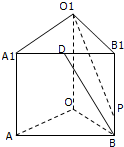已知在直三棱柱ABO-A1B1O1中，OO1=4，OA=4，OB=3，∠AOB=90°，点D是线段A1B1的中点，点P是侧棱BB1上一点，若O1P与平面AOB所成的角正切值为
3
8
．
（1）求证：OP⊥BD；
（2）求二面角D-OP-B的余弦值．
函数f（x）=loga（x+1）的图象关于原点对称的图象的解析式是y=g（x），若a＞1且0≤x＜1时，关于x的方程2f（x）+g（x）-m=0有实数根，则实数m取值范围是
 
．
已知不同的平面α、β和不同的直线m、n，有下列四个命题
①若m∥n，m⊥α，则n⊥α；
②若m⊥α，m⊥β，则α∥β；
③若m⊥α，m∥n，n?β，则α⊥β；
④若m∥α，α∩β=n，则m∥n，
其中正确命题的个数是（　　）
A、4个B、3个C、2个D、1个
函数y=cos（
π
3
-
1
2
x）的单调递增区间为
 
．
已知椭圆C的两个焦点坐标分别为（-4，0）和（4，0）且椭圆经过点P（5，0）求椭圆C的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网