题目内容
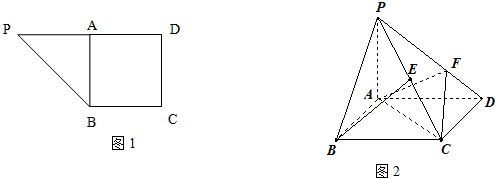
已知直角梯形PDCB中(如图1),PD=2,DC=BC=1,A为PD的中点,
将△PAB沿AB折起,使面PAB⊥面ABCD(如图2),点F在线段PD上,PF=2FD.
(1)求异面直线BP与CF所成角的余弦值;
(2)求二面角D-AC-F的余弦值;
(3)在四棱锥P-ABCD的棱PC上是否存在一点E,使得BE∥平面AFC,若存在,求出E点的位置,若不存在,请说明理由.
将△PAB沿AB折起,使面PAB⊥面ABCD(如图2),点F在线段PD上,PF=2FD.
(1)求异面直线BP与CF所成角的余弦值;
(2)求二面角D-AC-F的余弦值;
(3)在四棱锥P-ABCD的棱PC上是否存在一点E,使得BE∥平面AFC,若存在,求出E点的位置,若不存在,请说明理由.

考点:二面角的平面角及求法,异面直线及其所成的角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)由已知得PA⊥AB,从而PA⊥面ABCD,以A为原点,建立空间直角坐标系,利用向量法能求出异面直线BP与CF所成角的余弦值.
(2)由已知,得
=(0,0,1)为平面ACD的法向量,求出平面AFC的法向量,利用向量法能求出二面角D-AC-F的余弦值.
(3)法一:连接BD,交AC于O,取PF中点G,连BG,EG,FO,由已知得EG∥FC,OF∥BG,从而得到BE∥平面AFC.
(3)法二:假设在四棱锥P-ABCD的棱PC上存在一点E,使得BE∥平面AFC,设CE=λCP,由
=
+
,得
=(-λ,1-λ,λ),由此利用向量法能推导出存在PC的中点E,使得BE∥平面AFC.
(2)由已知,得
| AP |
(3)法一:连接BD,交AC于O,取PF中点G,连BG,EG,FO,由已知得EG∥FC,OF∥BG,从而得到BE∥平面AFC.
(3)法二:假设在四棱锥P-ABCD的棱PC上存在一点E,使得BE∥平面AFC,设CE=λCP,由
| BE |
| BC |
| CE |
| BE |
解答:
 (本小题满分14分)
(本小题满分14分)
解:(1)依题意知:PA⊥AB.
又∵面PAB⊥面ABCD,面PAB∩面ABCD=AB,PA?面PAB,
∴PA⊥面ABCD.…(2分)
又∵AD⊥AB.∴以A为原点,建立如图所示的坐标系,…(3分)
则A(0,0,0),B(1,0,0),C(1,1,0),
D(0,1,0),P(0,0,1).…(4分)
由于
=2
,
∴
=
+
=(0,0,1)+(0,
,-
)=(0,
,
),
即F(0,
,
).…(5分)
∴
=(-1,0,1),
=(-1,-
,
).
∴cos<
,
>=
=
=
.…(6分)
(2)由已知,得
=(0,0,1)为平面ACD的法向量.…(7分)
设平面AFC的法向量为
=(x,y,z),
则
,即
,…(8分)
令z=2,则x=1,y=-1,即
=(1,-1,2).…(9分)
二面角D-AC-F的平面角为θ,
则cosθ=
=
=
.…(10分)
(3)方法一:存在PC的中点E,使得:BE∥平面AFC,
证明如下:
连接BD,交AC于O,取PF中点G,连BG,EG,FO.
在△PCF中,E,G分别为PC,PF中点,则EG∥FC.…(11分)
在△BDG中,O,F分别为BD,DG中点,则OF∥BG.…(12分)
所以平面BEG∥平面FAC.
又BE?平面BEG,
所以BE∥平面AFC.…(14分)
方法二:假设在四棱锥P-ABCD的棱PC上存在一点E,使得BE∥平面AFC,
不妨设:CE=λCP,…(11分)
由
=
+
,得
=(-λ,1-λ,λ).…(12分)
由(2)知平面AFC的法向量
=(1,-1,2),
由
•
=0得λ=
.…(13分)
故存在PC的中点E,使得BE∥平面AFC.…(14分)
 (本小题满分14分)
(本小题满分14分)解:(1)依题意知:PA⊥AB.
又∵面PAB⊥面ABCD,面PAB∩面ABCD=AB,PA?面PAB,
∴PA⊥面ABCD.…(2分)
又∵AD⊥AB.∴以A为原点,建立如图所示的坐标系,…(3分)
则A(0,0,0),B(1,0,0),C(1,1,0),
D(0,1,0),P(0,0,1).…(4分)
由于
| PF |
| FD |
∴
| AF |
| AP |
| 2 |
| 3 |
| PD |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
即F(0,
| 2 |
| 3 |
| 1 |
| 3 |
∴
| BP |
| CF |
| 1 |
| 3 |
| 1 |
| 3 |
∴cos<
| BP |
| CF |
| ||||
|
| ||||||
|
2
| ||
| 11 |
(2)由已知,得
| AP |
设平面AFC的法向量为
| n |
则
|
|
令z=2,则x=1,y=-1,即
| n |
二面角D-AC-F的平面角为θ,
则cosθ=
| ||||
|
|
| 2 | ||
|
| ||
| 3 |
(3)方法一:存在PC的中点E,使得:BE∥平面AFC,
证明如下:
连接BD,交AC于O,取PF中点G,连BG,EG,FO.
在△PCF中,E,G分别为PC,PF中点,则EG∥FC.…(11分)
在△BDG中,O,F分别为BD,DG中点,则OF∥BG.…(12分)
所以平面BEG∥平面FAC.
又BE?平面BEG,
所以BE∥平面AFC.…(14分)
方法二:假设在四棱锥P-ABCD的棱PC上存在一点E,使得BE∥平面AFC,
不妨设:CE=λCP,…(11分)
由
| BE |
| BC |
| CE |
| BE |
由(2)知平面AFC的法向量
| n |
由
| BE |
| n |
| 1 |
| 2 |
故存在PC的中点E,使得BE∥平面AFC.…(14分)
点评:本题考查异面直线BP与CF所成角的余弦值的求法,考查二面角D-AC-F的余弦值的求法,考查在四棱锥P-ABCD的棱PC上是否存在一点E,使得BE∥平面AFC的判断与证明,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在椭圆
+
=1(a>b>0)中,F1、F2分别是其左右焦点,若椭圆上存在点P使得|PF1|-2|PF2|=a,则该椭圆的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(
| ||
B、(0,
| ||
C、[
| ||
D、[
|
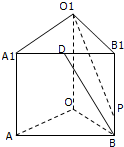 已知在直三棱柱ABO-A1B1O1中,OO1=4,OA=4,OB=3,∠AOB=90°,点D是线段A1B1的中点,点P是侧棱BB1上一点,若O1P与平面AOB所成的角正切值为
已知在直三棱柱ABO-A1B1O1中,OO1=4,OA=4,OB=3,∠AOB=90°,点D是线段A1B1的中点,点P是侧棱BB1上一点,若O1P与平面AOB所成的角正切值为