题目内容
已知四棱锥A-BCDE的底面是边长为2的正方形，面ABC⊥底面BCDE，且AB=AC=2，则四棱锥A-BCDE外接球的表面积为 ．
考点：球的体积和表面积,球内接多面体
专题：空间位置关系与距离
分析：如图所示，连接CE，BD，相交于点O1，过点O1作OO1⊥平面BCDE．设等边三角形ABC的中心为O2点，过O2点作OO2⊥平面ABC，点O为OO2与OO1的交点，则点O为四棱锥A-BCDE外接球的球心．利用正方形与等边三角形的有关知识即可得出四棱锥A-BCDE外接球的半径R，再利用球的表面积计算公式即可得出．
解答：
解：如图所示，
连接CE，BD，相交于点O1，过点O1作OO1⊥平面BCDE．
设等边三角形ABC的中心为O2点，过O2点作OO2⊥平面ABC，点O为OO2与OO1的交点，
则点O为四棱锥A-BCDE外接球的球心．
∵底面是边长为2的正方形，∴O1E=
．
由△ABC是边长为2的等边三角形，可得OO1=
×
．
∴四棱锥A-BCDE外接球的半径R=
=
=
．
∴四棱锥A-BCDE外接球的表面积=4πR2=
．
故答案为：
．
连接CE，BD，相交于点O1，过点O1作OO1⊥平面BCDE．
设等边三角形ABC的中心为O2点，过O2点作OO2⊥平面ABC，点O为OO2与OO1的交点，
则点O为四棱锥A-BCDE外接球的球心．
∵底面是边长为2的正方形，∴O1E=
| 2 |
由△ABC是边长为2的等边三角形，可得OO1=
| 1 |
| 3 |
| 3 |
∴四棱锥A-BCDE外接球的半径R=
O
|
(
|
|
∴四棱锥A-BCDE外接球的表面积=4πR2=
| 28π |
| 3 |
故答案为：
| 28π |
| 3 |
点评：本题考查了线面由于面面垂直的性质、正方形与等边三角形的性质、勾股定理、球的表面积计算公式，考查了空间想象能力，考查了推理能力与计算能力，属于难题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若tanα=lg（10a），tanβ=lg（
），且α+β=
，则实数a的值为（ ）
| 1 |
| a |
| π |
| 4 |
| A、1 | ||
B、
| ||
C、1或
| ||
| D、1或10 |
动点E在正方体ABCD-A1B1C1D1的棱BC上，F是CD的中点，则二面角C1-EF-C的余弦值的取值范围是（ ）
A、（0，
| ||||
B、（
| ||||
C、（0，
| ||||
D、（0，
|
在椭圆
+
=1（a＞b＞0）中，F1、F2分别是其左右焦点，若椭圆上存在点P使得|PF1|-2|PF2|=a，则该椭圆的离心率的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、（
| ||
B、（0，
| ||
C、[
| ||
D、[
|
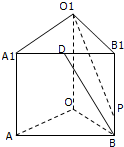已知在直三棱柱ABO-A1B1O1中，OO1=4，OA=4，OB=3，∠AOB=90°，点D是线段A1B1的中点，点P是侧棱BB1上一点，若O1P与平面AOB所成的角正切值为