题目内容
5.设定义在R上的函数f(x)对于任意x,y都有f(x+y)=f(x)+f(y)成立,且f(1)=-2,当x>0时,f(x)<0.(1)判断f(x)在R上的单调性,并加以证明;
(2)当-2015≤x≤2015时,不等式f(x)≤k恒成立,求实数k的取值范围.
分析 (1)令x=y=0求出f(0)=0,再令y=-x代入式子化简,结合函数奇偶性的定义,可得f(x)是奇函数;
设x1<x2,结合f(x+y)=f(x)+f(y)可得f(x2-x1)=f(x2)+f(-x1)=f(x2)-f(x1),由x>0时,有f(x)>0,可得f(x2)>f(x1),证明函数在R上单调递减;
(3)再利用赋值法和条件,分别求出函数最大值,再由不等式恒成立思想可得k的范围.
解答 解:(1)f(x)在R上单调递减.
理由如下:令x=y=0,可得f(0)=0,
令y=-x,则f(0)=f(-x)+f(x),
∴f(-x)=-f(x),∴f(x)为奇函数.
设x1<x2,令y=-x1,x=x2
则f(x2-x1)=f(x2)+f(-x1)=f(x2)-f(x1),
因为x>0时,f(x)<0,
故f(x2-x1)<0,即f(x2)-f(x1)<0.
∴f(x2)<f(x1),
∴f(x)在R上单调递减;
(2)f(x)在[-2015,2015]上单调递减,
∴x=-2015时,f(x)有最大值,
f(-2015)=-f(2015)=-2015f(1)
=-2015×(-2)=4030.
不等式f(x)≤k恒成立,
即有k≥4030.
点评 本题考查抽象函数的性质,涉及函数奇偶性、单调性的判断,以及函数最值,解此类题目,注意赋值法的运用.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
18.已知集合A=﹛-3,0,3﹜,B=﹛x|x2-2x-3=0﹜,则A∩B=( )
| A. | ∅ | B. | {3} | C. | {0} | D. | {-2} |
10.已知i是虚数单位,z=1+i,则复数$\frac{1}{z}$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中至少有1门不相同的概率等于( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
 ,集合
,集合 .
. ;
;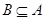 ,求实数
,求实数 的取值范围.
的取值范围. 某校甲、乙两个数学特长小组中分别有5名学生,他们在某次竞赛中取得的成绩(满分100分)的茎叶图如图所示:
某校甲、乙两个数学特长小组中分别有5名学生,他们在某次竞赛中取得的成绩(满分100分)的茎叶图如图所示: