题目内容
12.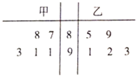 某校甲、乙两个数学特长小组中分别有5名学生,他们在某次竞赛中取得的成绩(满分100分)的茎叶图如图所示:
某校甲、乙两个数学特长小组中分别有5名学生,他们在某次竞赛中取得的成绩(满分100分)的茎叶图如图所示:(Ⅰ)计算甲组5名学生的成绩的平均数和方差;
(Ⅱ)用简单随机抽样方法从乙组5名同学中抽取2名,他们的成绩组成一个样本,求抽取的2名同学成绩的差值至少是4分的概率.
分析 (Ⅰ)根据茎叶图中的数据计算甲的平均数和方差即可;
(Ⅱ)用列举法求出基本事件数,计算出对应的概率即可.
解答 解:(Ⅰ)甲的平均数是
$\overline{{x}_{甲}}$=$\frac{1}{5}$(87+88+91+91+93)=90,
方差是${{s}_{甲}}^{2}$=$\frac{1}{5}$[(87-90)2+(88-90)2+(91-90)2+(91-90)2+(93-90)2]=$\frac{24}{5}$;
(Ⅱ)从乙组中抽取2名同学的成绩,所有的基本事件共有10种情况如下:
(85,89),(85,91),(85,92),(85,93),(89,91),
(89,92),(89,93),(91,92),(91,93),(92,93);
则抽取的2名同学的成绩差至少是4分的事件共5种情况如下;
(85,89),(85,91),(85,92),(85,93),(89,93);
故抽取的2名同学的成绩差值至少是4分的概率为P=$\frac{5}{10}$=$\frac{1}{2}$.
点评 本题考查了利用列举法求古典概型的概率问题,也考查了平均数与方差的计算问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.一个算法程序如图所示,则输出的n的值为( )
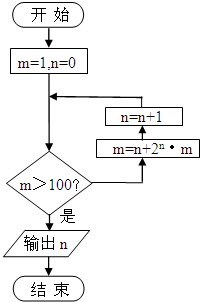

| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
7.等比数列{an}中,S10=10,S20=40,则S30=( )
| A. | 70 | B. | 90 | C. | 130 | D. | 160 |
17.已知△ABC,a=$\sqrt{2}$,b=$\sqrt{6}$,∠A=30°,则c=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$或$2\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 均不正确 |
4.将两颗骰子各掷一次,设事件A=“两个点数不相同”,B=“至少出现一个6点”,则概率P(A|B)等于( )
| A. | $\frac{10}{11}$ | B. | $\frac{5}{11}$ | C. | $\frac{5}{18}$ | D. | $\frac{5}{36}$ |
1.袋中装有5个小球,颜色分别是红色、黄色、白色、黑色和紫色,现从袋中随机抽取3个小球.设每个小球被抽到的机会均等,则抽到白球或黑球的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{9}{10}$ |
 ,则
,则 ____________.
____________.