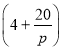题目内容
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,g(x)= ![]() (a∈R,e为自然对数的底数)
(a∈R,e为自然对数的底数)
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在![]() 上无零点,求a的最小值;
上无零点,求a的最小值;
(Ⅲ)若对任意给定的x0∈(0,e],在(0,e]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.
【答案】(1) f(x)的单调减区间为(0,2],单调增区间为[2,+∞);(2) 函数f(x)在![]() 上无零点,则a的最小值为2﹣4ln2;(3)a的范围是
上无零点,则a的最小值为2﹣4ln2;(3)a的范围是![]() .
.
【解析】试题分析:(Ⅰ)把a=1代入到f(x)中求出f′(x),令f′(x)>0求出x的范围即为函数的增区间,令f′(x)<0求出x的范围即为函数的减区间;
(Ⅱ)f(x)<0时不可能恒成立,所以要使函数在(0, ![]() )上无零点,只需要对x∈(0,
)上无零点,只需要对x∈(0, ![]() )时f(x)>0恒成立,列出不等式解出a大于一个函数,利用导数得到函数的单调性,根据函数的增减性得到这个函数的最大值即可得到a的最小值;
)时f(x)>0恒成立,列出不等式解出a大于一个函数,利用导数得到函数的单调性,根据函数的增减性得到这个函数的最大值即可得到a的最小值;
(Ⅲ)求出g′(x),根据导函数的正负得到函数的单调区间,即可求出g(x)的值域,而当a=2时不合题意;当a≠2时,求出f′(x)=0时x的值,根据x∈(0,e]列出关于a的不等式得到①,并根据此时的x的值讨论导函数的正负得到函数f(x)的单调区间,根据单调区间得到②和③,令②中不等式的坐标为一个函数,求出此函数的导函数,讨论导函数的正负得到函数的单调区间,根据函数的增减性得到此函数的最大值,即可解出②恒成立和解出③得到④,联立①和④即可解出满足题意a的取值范围.
试题解析:
(1)当a=1时,f(x)=x﹣1﹣2lnx,则f′(x)=1﹣![]() ,
,
由f′(x)>0,得x>2;
由f′(x)<0,得0<x<2.
故f(x)的单调减区间为(0,2],单调增区间为[2,+∞);
(2)因为f(x)<0在区间![]() 上恒成立不可能,
上恒成立不可能,
故要使函数![]() 上无零点,
上无零点,
只要对任意的![]() ,f(x)>0恒成立,即对
,f(x)>0恒成立,即对![]() 恒成立.
恒成立.
令![]() ,则
,则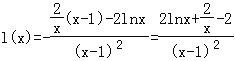 ,
,
再令![]() ,
,
则![]() ,故m(x)在
,故m(x)在![]() 上为减函数,于是
上为减函数,于是![]() ,
,
从而,l(x)>0,于是l(x)在![]() 上为增函数,所以
上为增函数,所以![]() ,
,
故要使![]() 恒成立,只要a∈[2﹣4ln2,+∞),
恒成立,只要a∈[2﹣4ln2,+∞),
综上,若函数f(x)在![]() 上无零点,则a的最小值为2﹣4ln2;
上无零点,则a的最小值为2﹣4ln2;
(3)g′(x)=e1﹣x﹣xe1﹣x=(1﹣x)e1﹣x,
当x∈(0,1)时,g′(x)>0,函数g(x)单调递增;
当x∈(1,e]时,g′(x)<0,函数g(x)单调递减.
又因为g(0)=0,g(1)=1,g(e)=ee1﹣e>0,
所以,函数g(x)在(0,e]上的值域为(0,1].
当a=2时,不合题意;
当a≠2时,f′(x)=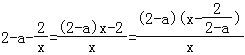 ,x∈(0,e]
,x∈(0,e]
当x=![]() 时,f′(x)=0.
时,f′(x)=0.
由题意得,f(x)在(0,e]上不单调,故![]() ,即
,即![]() ①
①
此时,当x变化时,f′(x),f(x)的变化情况如下:
x | (0, |
| ( |
f′(x) | ﹣ | 0 | + |
f(x) | ↘ | 最小值 | ↗ |
又因为,当x→0时,2﹣a>0,f(x)→+∞,
![]() ,
,
所以,对任意给定的x0∈(0,e],在(0,e]上总存在两个不同的xi(i=1,2),
使得f(xi)=g(x0)成立,当且仅当a满足下列条件:
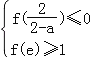 即
即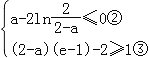
令h(a)=![]() ,
,
则h![]() ,令h′(a)=0,得a=0或a=2,
,令h′(a)=0,得a=0或a=2,
故当a∈(﹣∞,0)时,h′(a)>0,函数h(a)单调递增;
当![]() 时,h′(a)<0,函数h(a)单调递减.
时,h′(a)<0,函数h(a)单调递减.
所以,对任意![]() ,有h(a)≤h(0)=0,
,有h(a)≤h(0)=0,
即②对任意![]() 恒成立.
恒成立.
由③式解得:![]() .④
.④
综合①④可知,当a的范围是![]() 时,对任意给定的x0∈(0,e],在(0,e]上总存在两个不同的xi(i=1,2),使f(xi)=g(x0)成立.
时,对任意给定的x0∈(0,e],在(0,e]上总存在两个不同的xi(i=1,2),使f(xi)=g(x0)成立.